Câu hỏi:
2 năm trước
Tam thức bậc hai \(f\left( x \right) = {x^2} + \left( {1 - \sqrt 3 } \right)x - 8 - 5\sqrt 3 \):
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có \(f\left( x \right) = 0\, \Leftrightarrow \left[ \begin{array}{l}x = - 2 - \sqrt 3 \\x = 1 + 2\sqrt 3 \end{array} \right.\).
Bảng xét dấu
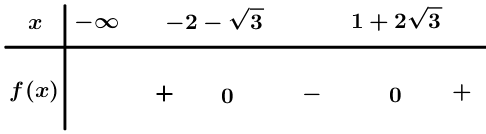
Dựa vào bảng xét dấu \(f\left( x \right) < 0\, \Leftrightarrow \, - 2 - \sqrt 3 < x < 1 + 2\sqrt 3 \).
Hướng dẫn giải:
Tìm các nghiệm của \(f\left( x \right)\), lập bảng xét dấu và kết luận.
Giải thích thêm:
Cách giải phương trình f(x)=0.
$\begin{array}{l}
\Delta = {\left( {1 - \sqrt 3 } \right)^2} - 4\left( { - 8 - 5\sqrt 3 } \right)\\
= 1 - 2\sqrt 3 + 3 + 32 + 20\sqrt 3 \\
= 36 + 18\sqrt 3 = 27 + 2.3\sqrt 3 .3 + 9\\
= {\left( {3\sqrt 3 } \right)^2} + 2.3\sqrt 3 .3 + {3^2}\\
= {\left( {3\sqrt 3 + 3} \right)^2}\\
\Rightarrow \sqrt \Delta = 3\sqrt 3 + 3\\
\Rightarrow \left[ \begin{array}{l}
x = \frac{{ - 1 + \sqrt 3 - 3\sqrt 3 - 3}}{2} = - 2 - \sqrt 3 \\
x = \frac{{ - 1 + \sqrt 3 + 3\sqrt 3 + 3}}{2} = 1 + 2\sqrt 3
\end{array} \right.
\end{array}$
