Câu hỏi:
2 năm trước
Tìm các giá trị của tham số m để phương trình $\dfrac{1}{2}{x^2} - 4\left| x \right| + 3 = {m^2}$ có 3 nghiệm thực phân biệt.
Trả lời bởi giáo viên
Đáp án đúng: c
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số $y = \dfrac{1}{2}{x^2} - 4\left| x \right| + 3 = \left\{ \begin{array}{l}\dfrac{1}{2}{x^2} - 4x + 3\,\,\,\left( {x \ge 0} \right)\\\dfrac{1}{2}{x^2} + 4x + 3\,\,\,\,\left( {x < 0} \right)\end{array} \right.$ và đường thẳng $y = {m^2}$ có tính chất song song với trục hoành.
Đồ thị hàm số $y = \dfrac{1}{2}{x^2} - 4\left| x \right| + 3$ được vẽ như sau :
+ Vẽ hai đồ thị hàm số trên cùng một hệ trục tọa độ.
+ Giữ nguyên nhánh bên phải trục tung của đồ thị hàm $y = \dfrac{1}{2}{x^2} - 4x + 3$ và xóa nhánh bên trái trục tung.
+ Giữ nguyên nhánh bên trái trục tung của đồ thị hàm số $y = \dfrac{1}{2}{x^2} + 4x + 3$ và xóa nhánh bên phải trục tung của đồ thị hàm số đó.
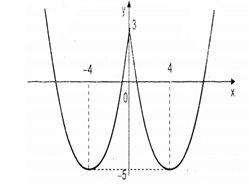
Dựa trên đồ thị ta thấy phương trình đã cho có $3$ nghiệm phân biệt khi và chỉ khi ${m^2} = 3 \Leftrightarrow m = \pm \sqrt 3 $.
Hướng dẫn giải:
- Vẽ đồ thị hàm số \(y = \dfrac{1}{2}{x^2} - 4x + 3\).
- Dựng đồ thị hàm số $y = \dfrac{1}{2}{x^2} - 4\left| x \right| + 3$ có được từ đồ thị hàm số vừa vẽ : Giữ nguyên phần đồ thị bên phải trục tung, xóa bỏ phần bên trái trục tung đồng thời lấy đối xứng phần đồ thị đó qua trục tung.
