Trả lời bởi giáo viên
Đáp án đúng: a
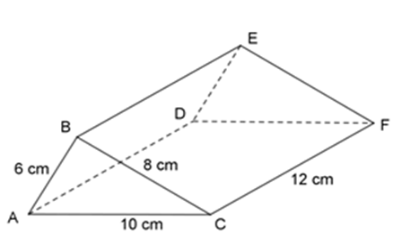
Ta có:
\(\begin{array}{l}A{B^2} + B{C^2} = {6^2} + {8^2} = 100\\A{C^2} = {10^2} = 100\\ \Rightarrow A{B^2} + B{C^2} = A{C^2}\end{array}\)
Áp dụng định lý đảo của định lý Pitago ta có tam giác $ABC$ là tam giác vuông tại $B$ .
Vì $ABC.DEF$ là hình lăng trụ đứng nên $2$ mặt đáy $ABC$ và $DEF$ song song và bằng nhau.
Suy ra tam giác $DEF$ là tam giác vuông tại $E$ .
Hướng dẫn giải:
- Áp dụng kiến thức định lý đảo của định lý Talet để chứng minh tam giác vuông.