Câu hỏi:
2 năm trước
Một vật dao động điều hòa với chu kỳ \(T\) và biên độ \(A\). Ban đầu vật ở vị trí cân bằng, khoảng thời gian ngắn nhất kể từ khi vật dao động đến thời điểm mà thế năng bằng 3 lần động năng là:
Trả lời bởi giáo viên
Đáp án đúng: c
+ Vị trí ban đầu: \(x = 0\)
+ Vị trí: \(\left\{ \begin{array}{l}{W_t} = 3{W_d}\\W = {W_t} + {W_d}\end{array} \right. \to {W_t} = \dfrac{3}{4}W \to x = \pm \dfrac{{A\sqrt 3 }}{2}\)
Vẽ trên vòng tròn lượng giác, ta được:
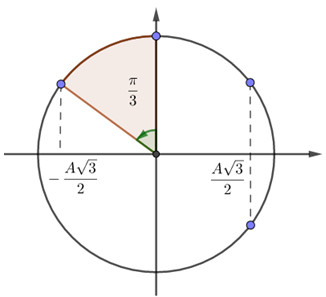
Khoảng thời gian ngắn nhất kể từ khi vật dao động đến thời điểm mà thế năng bằng 3 lần động năng ứng với góc quét \(\Delta \varphi = \dfrac{\pi }{3}\)
Mặt khác, ta có:
\(\begin{array}{l}\Delta \varphi = \omega \Delta t \leftrightarrow \dfrac{\pi }{3} = \dfrac{{2\pi }}{T}\Delta t\\ \to \Delta t = \dfrac{T}{6}\end{array}\)
=> Khoảng thời gian ngắn nhất kể từ khi vật dao động đến thời điểm mà thế năng bằng 3 lần động năng là \(\dfrac{T}{6}\)
Hướng dẫn giải:
+ Áp dụng biểu thức xác định cơ năng: \({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_{\rm{d}}}\)
+ Sử dụng vòng tròn lượng giác và biểu thức: \(\Delta \varphi = \omega \Delta t\)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
