Câu hỏi:
2 năm trước
Một hình hộp chữ nhật có đường chéo lớn bằng \(16,25cm\), các kích thước của đáy bằng \(5cm\) và \(12cm\). Tính thể tích của hình hộp chữ nhật đó.
Trả lời bởi giáo viên
Đáp án đúng: a
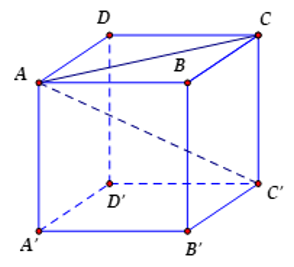
Vì \(ABCD\) là hình chữ nhật nên \(AD = BC = 5cm;\,AB = DC = 12\,cm\).
Áp dụng định lý Pytago cho tam giác vuông \(ADC\) ta được:
\(AC = \sqrt {{5^2} + {{12}^2}} = 13\,cm\)
Ta có: \(CC' \bot \left( {ABCD} \right)\) nên \(CC' \bot CD\).
Áp dụng định lý Pytago cho tam giác vuông \(AC'C\) ta được:
\(CC' = \sqrt {AC{'^2} - A{C^2}} \) \( = \sqrt {16,{{25}^2} - {{13}^2}} = 9,75\,cm\)
Thể tích của hình hộp chữ nhật bằng:
\(5.12.9,75 = 585\left( {c{m^3}} \right)\).
Hướng dẫn giải:
+ Từ các điều kiện đề bài tìm chiều cao của hình hộp chữ nhật bằng định lý Pytago.
+ Sử dụng công thức thể tích hình hộp chữ nhật để tính toán.
