Một dây đàn hồi $AB$ đầu $A$ được rung nhờ một dụng cụ để tạo thành sóng dừng trên dây, biết Phương trình dao động tại đầu $A$ là $u_A= acos100πt$. Quan sát sóng dừng trên sợi dây ta thấy trên dây có những điểm không phải là điểm bụng dao động với biên độ $b$ \((b \ne 0)\) cách đều nhau và cách nhau khoảng $1m$. Giá trị của $b$ và tốc truyền sóng trên sợi dây lần lượt là:
Trả lời bởi giáo viên
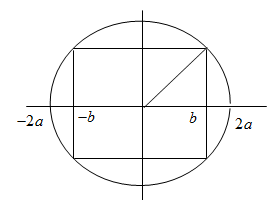
Các điểm dao động với biên độ \(b \ne 0\) và \(b \ne 2a\) (tức là không phải là điểm nút và điểm bụng) cách đều nhau thì khoảng cách giữa hai điểm bằng $\dfrac{\lambda }{4} = 1m \to \lambda = 4m$
Do đó $v = λf = 4.50 = 200 (m/s)$
Theo hình vẽ ta thấy
\(b =\dfrac{{2a\sqrt 2 }}{2}= a\sqrt 2 \)
(Biên độ của bụng sóng là $2a$)
Hướng dẫn giải:
+ Sử dụng vòng tròn lượng giác
+ Áp dụng công thức tính tốc độ truyền sóng: $v = λf$

