Một con lắc lò xo gồm lò xo nhẹ có độ cứng 25N/m một đầu được gắn với hòn bi nhỏ có khối lượng 100g. Tại thời điểm t = 0, thả cho con lắc rơi tự do sao cho trục của lò xo luôn nằm theo phương thẳng đứng và vật nặng ở phía dưới lò xo. Đến thời điểm \({t_1} = 0,02\sqrt {30} \,s\) thì đầu trên của lò xo bị giữ lại đột ngột. Sau đó vật dao động điều hòa. Lấy g = 10m/s2. Tại thời điểm \({t_2} = {t_1} + 0,1\,\left( s \right)\), tốc độ của hòn bi gần giá trị nào sau đây?
Trả lời bởi giáo viên
Tần số góc: \(\omega = \sqrt {\dfrac{k}{m}} = \sqrt {\dfrac{{25}}{{0,1}}} = 5\pi \,\left( {rad/s} \right) \Rightarrow T = 0,4s\)
Khi thả rơi tự do con lắc thì nó ở trạng thái không biến dạng và vận tốc của nó tại thời điểm \({t_1} = 0,02\sqrt {30} \,s\)là:
\(v = gt = 10.0,02\sqrt {30} = 0,2\sqrt {30} m/s\)
Sau khi đột ngột giữ lại đầu trên của con lắc thì con lắc sẽ dao động quanh vị trí cân bằng. Tại vị trí này lò xo giãn: \(\Delta {l_0} = \dfrac{{mg}}{k} = \dfrac{{0,1.10}}{{25}} = 0,04m = 4cm\)
Chọn trục tọa độ thẳng đứng chiều dương hướng xuống dưới, gốc tọa độ tại VTCB thì li độ của lò xo tại thời điểm lò xo bị giữ là: \(x = - \Delta {l_0} = - 4cm\)
Biên độ dao động của con lắc:
\(A = \sqrt {{x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}} = \sqrt {{{\left( { - 0,04} \right)}^2} + \dfrac{{{{\left( {0,2\sqrt {30} } \right)}^2}}}{{{{\left( {5\pi } \right)}^2}}}} = 8cm\)
Thời điểm \({t_2} = {t_1} + 0,1\,\left( s \right) = {t_1} + \dfrac{T}{4} \Rightarrow \Delta t = \dfrac{T}{4}\)
Biểu diễn trên VTLG ta có:
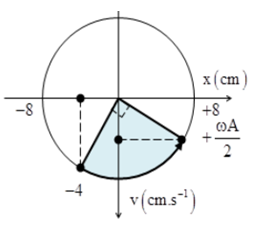
Từ VTLG ta có: \(v = \dfrac{{\omega A}}{2} = \dfrac{{5\pi .8}}{2} = 20\pi \approx 62,8cm/s\)
Chọn A.
Hướng dẫn giải:
Tần số góc: \(\omega = \sqrt {\dfrac{k}{m}} \Rightarrow T = \dfrac{{2\pi }}{\omega }\)
Vận tốc của vật rơi tự do: \(v = g.t\)
Độ giãn của lò xo tại VTCB: \(\Delta {l_0} = \dfrac{{mg}}{k}\)
Biên độ dao động: \(A = \sqrt {{x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}} \)
Sử dụng VTLG tính ra được tốc độ của vật tại t2.

