Một con lắc đơn gồm sợi dây mảnh dài \(l = 1m\), vật có khối lượng \(m = 100\sqrt 3 g\) tích điện \(q = {10^{ - 5}}\left( C \right)\). Treo con lắc đơn trong điện trường đều có phương vuông góc với gia tốc trọng trường \(\overrightarrow g \) và có độ lớn \(E = {10^5}V/m\). Kéo vật theo chiều của vec tơ điện trường sao cho góc tạo bởi dây treo của con lắc và \(\overrightarrow g \) bằng \({60^0}\) rồi thả nhẹ để vật dao động. Lực căng cực đại của dây treo là:
Trả lời bởi giáo viên
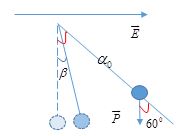
+ VTCB mới của con lắc là vị trí mà dây treo hợp với phương thẳng đứng góc \(\beta \) sao cho:
\(\tan \beta = \dfrac{{\left| q \right|E}}{{mg}} = \dfrac{{{{10}^{ - 5}}{{.10}^5}}}{{100\sqrt 3 {{.10}^{ - 3}}.10}} = \dfrac{1}{{\sqrt 3 }} \Rightarrow \beta = {30^0}\left( {rad} \right)\)
+ Kéo con lắc đơn ra sao cho gia tốc trọng trường \(g\) tạo với dây treo của con lắc một góc ${60^0}$
=> CLĐ sẽ dao động với biên độ \({\alpha _0} = {60^0}{\text{ - }}\beta = {60^0} - {30^0} = {30^0}\).
+ Gia tốc trọng trường hiệu dụng \(g' = \sqrt {{g^2} + {a^2}} = \sqrt {{g^2} + {g^2}{{\tan }^2}\beta } = \dfrac{{2g}}{{\sqrt 3 }}\)
Lực căng dây cực đại của con lắc đơn: \({T_{\max }} = mg'\left( {3 - 2\cos {\alpha _0}} \right) = 100\sqrt 3 {.10^{ - 3}}.\dfrac{{2.10}}{{\sqrt 3 }}.\left( {3 - 2\cos {{30}^0}} \right) = 2,54N\)
Hướng dẫn giải:
+ Vận dụng biểu thức tính lực điện: \({F_d} = qE\)
+ Sử dụng công thức tính lực căng dây cực đại: \({T_{{\rm{max}}}} = mg\left( {3 - 2\cos {\alpha _0}} \right)\)

