Câu hỏi:
2 năm trước
Một cái máng nước sâu \(20 cm\) rộng \(10 cm\) có hai thành bên thẳng đứng. Lúc máng cạn nước thì bóng râm của thành \(A\) kéo dài tới đúng chân thành \(B\) đối diện. Người ta đổ nước vào máng đến một độ cao \(h\) thì bóng của thành \(A\) ngắn bớt đi \(2 cm\) so với trước. Biết chiết suất của nước là \(n = \dfrac{4}{3}\). \(h = ?\)
Trả lời bởi giáo viên
Đáp án đúng: c
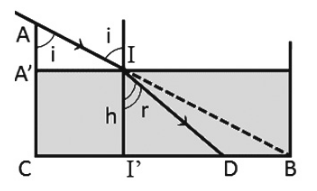
Ta có: \(\tan i = \dfrac{{CI'}}{{AA'}} = \dfrac{{CB}}{{AC}} = \dfrac{{10}}{{20}} = \dfrac{1}{2} \to i = 26,{57^0}\)
Theo định luật khúc xạ ánh sáng, ta có:
\(\begin{array}{l}{n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\\ \Rightarrow {\rm{sinr}} = \dfrac{{{n_1}\sin i}}{{{n_2}}} = \dfrac{{1.sin26,{{57}^0}}}{{\dfrac{4}{3}}} = 0,335\\ \Rightarrow r = 19,{6^0}\\ \Rightarrow {\mathop{\rm t}\nolimits} {\rm{anr}} = 0,356\end{array}\)
Mặt khác, từ hình ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}\tan i = \dfrac{{I'B}}{h}\\{\mathop{\rm t}\nolimits} {\rm{anr}} = \dfrac{{I'B - DB}}{h}\end{array} \right.\\ \Rightarrow \dfrac{{\tan i}}{{{\mathop{\rm t}\nolimits} {\rm{anr}}}} = \dfrac{{I'B}}{{I'B - DB}} = \dfrac{{0,5}}{{0,356}} = 1,4\\ \Rightarrow I'B = 3,5.DB = 3,5.2 = 7cm\\ \Rightarrow h = \dfrac{{I'B}}{{\tan i}} = \dfrac{7}{{0,5}} = 14cm\end{array}\)
Hướng dẫn giải:
+ Sử dụng các hệ thức lượng trong tam giác
+ Vận dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
