Câu hỏi:
2 năm trước
Một cái chậu hình chữ nhật có đáy phẳng nằm ngang chứa đầy nước. Một người nhìn vào điểm giữa của mặt nước theo phương hợp với phương thẳng đứng một góc \({45^0}\) thì vừa vặn nhìn thấy một điểm nằm trên giao tuyến của thành chậu và đáy chậu. Tính độ sâu của chậu. Cho biết chiết suất của nước là \(n = \dfrac{4}{3}\), chiều dài của chậu là \(30cm\).
Trả lời bởi giáo viên
Đáp án đúng: b
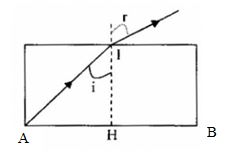
Ta có:
\(AB = 30cm\)
\(AH = \dfrac{{AB}}{2} = 15cm\)
Theo đề bài, ta có: \(r = {45^0}\)
+ Áp dụng định luật khúc xạ ánh sáng, ta có:
\(\begin{array}{l}{n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\\ \Rightarrow \dfrac{4}{3}\sin i = 1.\sin {45^0}\\ \Rightarrow \sin i = \dfrac{{3\sqrt 2 }}{8}\end{array}\)
Từ hình, ta có:
\(\begin{array}{l}\sin i = \dfrac{{AH}}{{IA}} = \dfrac{{AH}}{{\sqrt {I{H^2} + A{H^2}} }} = \dfrac{{3\sqrt 2 }}{8}\\ \Leftrightarrow \dfrac{{15}}{{\sqrt {{h^2} + {{15}^2}} }} = \dfrac{{3\sqrt 2 }}{8}\\ \Rightarrow h \approx 24cm\end{array}\)
Hướng dẫn giải:
+ Vẽ đường truyền tia sáng qua lưỡng chất phẳng
+ Sử dụng hệ thức lượng trong tam giác
