Trả lời bởi giáo viên
Đáp án đúng: a
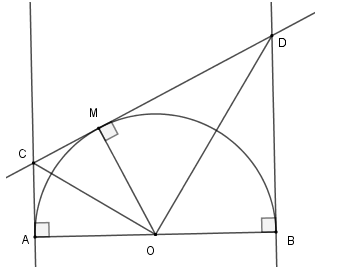
Xét nửa \(\left( O \right)\) có \(MC\) và \(AC\) là hai tiếp tuyến cắt nhau tại \(C\) nên \(OC\) là phân giác \(\widehat {MOA}\) do đó \(\widehat {AOC} = \widehat {COM}\)
Lại có \(MD\) và \(BD\) là hai tiếp tuyến cắt nhau tại \(D\) nên \(OD\) là phân giác \(\widehat {MOB}\) do đó \(\widehat {BOD} = \widehat {DOM}\)
Từ đó \(\widehat {AOC} + \widehat {BOD} = \widehat {COM} + \widehat {MOD}\)\( = \dfrac{{\widehat {AOC} + \widehat {BOD} + \widehat {COM} + \widehat {MOD}}}{2} = \dfrac{{180^\circ }}{2} = 90^\circ \)
Nên \(\widehat {COD} = 90^\circ \)hay \(\Delta COD\) vuông tại \(O\) có \(OM\) là đường cao nên \(MC.MD = O{M^2}\).
Mà \(OM = R = \dfrac{{AB}}{2} = 5cm\) nên \(MC.MD = 25\,\left( {c{m^2}} \right)\)
Hướng dẫn giải:
Sử dụng tính chất hai tiếp tuyến cắt nhau và hệ thức lượng trong tam giác vuông
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
