Hai nguồn song kết hợp A và B dao động theo phương trình \(u_A=a\cos(\omega t)\) \({u_B} = a\cos (\omega t + \varphi )\). Biết điểm không dao động gần trung điểm I của AB nhất một đoạn \(\dfrac{\lambda }{3}\). Tìm \(\varphi \)
Trả lời bởi giáo viên
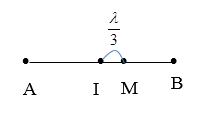
Xét điểm M trên AB; \(AM{\rm{ }} = {\rm{ }}{d_1};{\rm{ }}BM{\rm{ }} = {\rm{ }}{d_2}\left( {{\rm{ }}{d_1} > {\rm{ }}{d_2}} \right)\)
\(\begin{array}{l}\left\{ \begin{array}{l}{d_1} = AM = \dfrac{{AB}}{2} + IM\\{d_2} = BM = \dfrac{{AB}}{2} - IM\end{array} \right.\\ \Rightarrow {d_1} - {d_2} = AM - BM = 2IM = \dfrac{{2\lambda }}{3}\end{array}\)
Sóng truyền từ A , B đến M
\(\begin{array}{l}{u_{AM}} = acos(\omega t - \dfrac{{2\pi {d_1}}}{\lambda });{u_{BM}} = acos(\omega t - \dfrac{{2\pi {d_2}}}{\lambda } + \varphi )\\{u_M} = 2acos(\dfrac{{\pi ({d_1} - {d_2})}}{\lambda } + \dfrac{\varphi }{2})cos(\omega t - \dfrac{{\pi ({d_2} + {d_1})}}{\lambda } + \dfrac{\varphi }{2})\end{array}\)
Điểm M không dao động khi: \(cos(\dfrac{{\pi ({d_1} - {d_2})}}{\lambda } + \dfrac{\varphi }{2}) = 0\)
\(\dfrac{{\pi ({d_1} - {d_2})}}{\lambda } + \dfrac{\varphi }{2} = \dfrac{\pi }{2} + k\pi \to {d_1}-{d_2} = (\dfrac{1}{2} - \dfrac{\varphi }{{2\pi }} + k)\lambda \)
Điểm M gần trung điểm I nhất ứng với (trường hợp hình vẽ) k = 0
\(\begin{array}{l}(\dfrac{1}{2} - \dfrac{\varphi }{{2\pi }})\lambda = \dfrac{{2\lambda }}{3}\\ \Rightarrow \dfrac{1}{2} - \dfrac{\varphi }{{2\pi }} = \dfrac{2}{3} \Rightarrow \varphi = - \dfrac{\pi }{3}\end{array}\).
Hướng dẫn giải:
+ Viết phương trình dao động tổng hợp tại một điểm trong trường giao thoa.
+ Điểm không dao động khi biên độ dao động tổng hợp tại điểm đó = 0

