Xét số phức \(z\) thỏa mãn \(\left| {z + 2 - i} \right| + \left| {z - 4 - 7i} \right| = 6\sqrt 2 \). Gọi \(m,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của \(\left| {z - 1 + i} \right|\). Tính \(P = m + M\).

Gọi $z=x+yi\left( x,y\in R \right)$

Trên mặt phẳng tọa độ $Oxy$ gọi $P\left( {x;y} \right)$ là điểm biểu diễn của số phức $z$

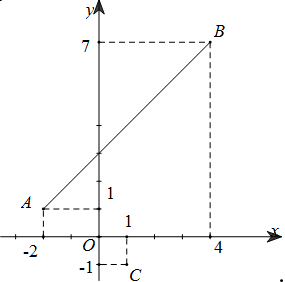
Gọi $A\left( {-2;1} \right),B\left( {4;7} \right)$ thì

$\begin{array}{l}AB = 6\sqrt 2  = \left| {z + 2 - i} \right| + \left| {z - 4 - 7i} \right|\\ = \sqrt {{{\left( {x + 2} \right)}^2} + {{\left( {y - 1} \right)}^2}}  + \sqrt {{{\left( {x - 4} \right)}^2} + {{\left( {y - 7} \right)}^2}}  = PA + PB\end{array}$

Suy ra tập hợp các điểm $P$ thỏa mãn chính là đoạn thẳng AB

Có $\left| {z - 1 + i} \right| = \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y + 1} \right)}^2}}  = PC$ với $C\left( {1;-1} \right)$

Do đó \(P{C_{\min }}\) khi \(P\) là hình chiếu của \(C\) lên \(AB\) và \(P{C_{\max }}\) khi \(P \equiv B\)

Suy ra $M = CB = \sqrt {73} $.

Ta có: \(AB:\dfrac{{x + 2}}{{4 + 2}} = \dfrac{{y - 1}}{{7 - 1}} \Leftrightarrow x - y + 3 = 0\)\( \Rightarrow m=d\left( {C,AB} \right) = \dfrac{{\left| {1 - \left( { - 1} \right) + 3} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \dfrac{5}{{\sqrt 2 }}\)

$\Rightarrow M + m = \dfrac{{5\sqrt 2  + 2\sqrt {73} }}{2}$