Câu hỏi:
2 năm trước
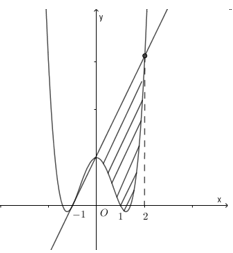
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: a
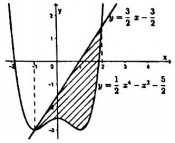
Dựa vào đồ thị hàm số ta thấy: Đường thẳng \(y = \dfrac{3}{2}x - \dfrac{3}{2}\) cắt đồ thị hàm số \(y = \dfrac{1}{2}{x^4} - {x^2} - \dfrac{5}{2}\) tại hai điểm phân biệt có hoành độ lần lượt là \(x = - 1,\,\,x = 2\).
Do đó phần hình phẳng gạch chéo được giới hạn bởi đồ thị hàm số \(y = \dfrac{1}{2}{x^4} - {x^2} - \dfrac{5}{2}\), \(y = \dfrac{3}{2}x - \dfrac{3}{2}\), đường thẳng \(x = - 1\), \(x = 2\), và trong khoảng \(\left( { - 1;2} \right)\), đường thẳng \(y = \dfrac{3}{2}x - \dfrac{3}{2}\) luôn nằm phía trên đồ thị hàm số \(y = \dfrac{1}{2}{x^4} - {x^2} - \dfrac{5}{2}\). Do đó ta có: \(S = \int\limits_{ - 1}^2 {\left( {\dfrac{3}{2}x - \dfrac{3}{2} - \dfrac{1}{2}{x^4} + {x^2} + \dfrac{5}{2}} \right)dx} = \int\limits_{ - 1}^2 {\left( { - \dfrac{1}{2}{x^4} + {x^2} + \dfrac{3}{2}x + 1} \right)} \).
Hướng dẫn giải:
- Xác định các phần hình phẳng gạch chéo được giới hạn bởi các đường nào.
- Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\), đường thẳng \(x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Câu hỏi khác
- Bài tập nguyên hàm toán 12 có lời giải
- Bài tập tích phân các hàm số cơ bản toán 12 có lời giải
- Bài tập tích phân có lời giải MÔN TOÁN Lớp 12
- Bài tập sử dụng phương pháp đổi biến để tìm nguyên hàm có lời giải MÔN TOÁN Lớp 12
- Bài tập sử dụng phương pháp từng phần để tìm nguyên hàm có lời giải MÔN TOÁN Lớp 12
