
Điền số thích hợp vào ô trống:
Lúc \(8\) giờ $30$ phút ô tô thứ nhất đi từ A đến B với vận tốc $44$ km/giờ. Lúc $9$ giờ ô tô thứ hai đi từ B để đến A với vận tốc $56$ km/giờ. Hai xe gặp nhau lúc $10$ giờ $45$ phút.
Vậy độ dài quãng đường AB là
\(km\).
Trả lời bởi giáo viên
Lúc \(8\) giờ $30$ phút ô tô thứ nhất đi từ A đến B với vận tốc $44$ km/giờ. Lúc $9$ giờ ô tô thứ hai đi từ B để đến A với vận tốc $56$ km/giờ. Hai xe gặp nhau lúc $10$ giờ $45$ phút.
Vậy độ dài quãng đường AB là
\(km\).
Ta có sơ đồ chuyển động của hai xe như sau:
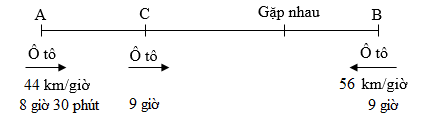
Thời gian ô tô thứ nhất đi trước ô tô thứ hai là:
$9$ giờ \( - \,8\) giờ $30$ phút \( = \,30\) phút
Đổi: $30$ phút \( = \,0,5\) giờ
Trong \(0,5\) giờ, ô tô đi được quãng đường AC dài là:
\(44 \times \,0,5 = 22 \;(km)\)
Thời gian đi để hai xe gặp nhau (kể từ khi ô tô thứ hai xuất phát) là:
$10$ giờ $45$ phút $ - \,9$ giờ $ = \,1$ giờ $45$ phút
Đổi $1$ giờ $45$ phút \( = \,1,75\) giờ
Tổng vận tốc của hai xe là:
\(44 + 56 = 100\) (km/giờ)
Quãng đường BC dài là:
\(100 \times 1,75 = 175\;(km)\)
Quãng đường AB dài là:
\(22 + 175 = 197\;(km)\)
Đáp số: \(197km\).
Vậy đáp án đúng điền vào ô trống là \(197\).
Hướng dẫn giải:
Theo đề bài, hai ô tô xuất phát không cùng lúc. Đến $9$ giờ thì hai xe mới cùng chuyển động. Để giải bài này ta làm như sau:
- Tính thời gian ô tô thứ nhất đi trước ô tô thứ hai: $9$ giờ \( - 8\) giờ $30$ phút \( = 30\) phút và đổi kết quả vừa tìm được sang dạng số thập phân có đơn vị là giờ.
- Tính quãng đường ô tô đi được trong \(30\) phút.
- Tính thời gian đi để gặp nhau ta lấy thời gian lúc gặp nhau trừ đi thời gian lúc ô tô thứ hai xuất phát: $10$ giờ $45$ phút $ - \,9$ giờ và đổi kết quả vừa tìm được sang dạng số thập phân có đơn vị là giờ.
- Tính tổng vận tốc hai xe.
- Tính quãng đường ô tô và xe máy chuyển động ngược chiều ta lấy tổng vận tốc nhân với thời gian đi để gặp nhau.
- Độ dài quãng đường AB bằng tổng quãng đường ô tô đi được trong \(30\) phút và quãng đường ô tô và xe máy chuyển động ngược chiều.





.png)


