Câu hỏi:
2 năm trước
Điền số thích hợp vào ô trống (dạng thu gọn nhất có thể):
Một thùng hàng hình hộp chữ nhật có tỉ số giữa chiều dài và chiều rộng là \(\dfrac{5}{3}\). Biết chiều dài hơn chiều rộng $36cm$ và chiều cao của thùng hàng bằng trung bình cộng độ dài chiều rộng và chiều dài.
Vậy thể tích của thùng hàng đó là
\(d{m^3}\).
Trả lời bởi giáo viên
Đáp án:
Một thùng hàng hình hộp chữ nhật có tỉ số giữa chiều dài và chiều rộng là \(\dfrac{5}{3}\). Biết chiều dài hơn chiều rộng $36cm$ và chiều cao của thùng hàng bằng trung bình cộng độ dài chiều rộng và chiều dài.
Vậy thể tích của thùng hàng đó là
\(d{m^3}\).
Theo bài ra ta có sơ đồ:
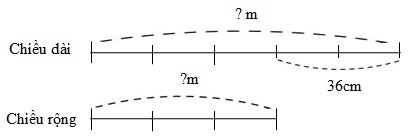
Theo sơ đồ, hiệu số phần bằng nhau là:
\(5 - 3 = 2\) (phần)
Chiều dài của thùng hàng là:
\(36 : 2 \times 5 = 90\,(cm)\)
Chiều rộng của thùng hàng là:
\(90 - 36 = 54\,(cm)\)
Chiều cao của thùng hàng là:
\((90 + 54):2 = 72\,(cm)\)
Thể tích của thùng hàng đó là:
\(90 \times 54 \times 72 = 349920\,(c{m^3})\)
\(349920c{m^3} = 349,92d{m^3}\)
Đáp số: \(349,92d{m^3}\).
Vậy đáp án đúng điền vào ô trống là \(349,92\).
Hướng dẫn giải:
- Tìm chiều dài, chiều rộng theo bài toán tìm hai số khi biết hiệu và tỉ số của hai số:
+ Vẽ sơ đồ biểu diễn chiều dài và chiều rộng: coi chiều rộng là \(3\) phần thì chiều dài là \(5\) phần.
+ Tìm hiệu số phần bằng nhau.
+ Tìm chiều dài = Hiệu : Hiệu số phần bằng nhau x số phần chỉ chiều dài.
+ Tìm chiều rộng = chiều dài - 36 cm.
- Tìm chiều cao ta lấy tổng độ dài chiều dài và chiều rộng chia cho \(2\).
- Tìm thể tích theo công thức: Thể tích = chiều dài × chiều rộng × chiều cao.
- Đổi đơn vị thể tích về đơn vị đề-xi-mét khối.
Một bể cá cảnh hình hộp chữ nhật có chiều dài $1,8m$; chiều rộng $0,6m$ và chiều cao \(0,9m\) . Hỏi người ta phải đổ vào trong bể cá cảnh đó bao nhiêu lít nước để lượng nước trong bể cao $0,6m$?
