Đề thi THPT QG 2022 – mã đề 124

Xét tất cả các số thực $x, y$ sao cho \({49^{9 - {y^2}}} \ge {a^{4x - {{\log }_7}{a^2}}}\) với mọi số thực dương \(a\). Giá trị lớn nhất của biểu thức \(P = {x^2} + {y^2} + 4x - 3y\) bằng

Ta có \({49^{9 - {y^2}}} \ge {a^{4x - {{\log }_7}{a^2}}}\)

\(\begin{array}{*{20}{l}}{ \Leftrightarrow {{\log }_7}{{49}^{9 - {y^2}}} \ge {{\log }_7}{a^{4x - {{\log }_7}{a^2}}}}\\{ \Leftrightarrow 2\left( {9 - {y^2}} \right) \ge \left( {4x - 2{{\log }_7}a} \right){{\log }_7}a}\\{ \Leftrightarrow 9 - {y^2} \ge 2x.{{\log }_7}a - {{\left( {{{\log }_7}a} \right)}^2}}\end{array}\)

\( \Leftrightarrow \log _7^2a - 2x{\log _7}a + 9 - {y^2} \ge 0,\forall a > 0\)

\( \Leftrightarrow {\Delta ^\prime } = {x^2} + {y^2} - 9 \le 0 \Leftrightarrow {x^2} + {y^2} \le 9\)

=> Tập các điểm thỏa mãn điều kiện trên là hình tròn \((C)\) tâm O bán kính R=3.

\(P = {x^2} + {y^2} + 4x - 3y\) \( \Leftrightarrow {(x + 2)^2} + {(y - \dfrac{3}{2})^2} = P + \dfrac{{25}}{4}\)

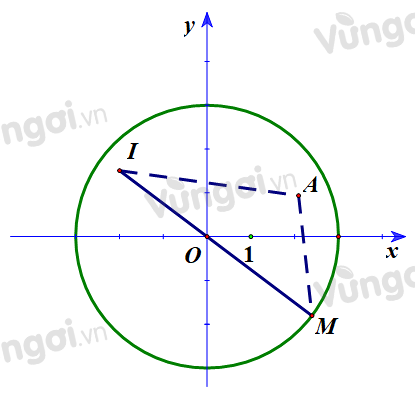
Gọi \(A(x;y)\) thuộc hình tròn \((C)\).

Ta thấy \(I(-2;\dfrac{3}{2})\) nằm trong đường tròn \((C)\).

\(P + \dfrac{25}{4} = I{A^2}\)

\( \Rightarrow I{A_{\max }} = IB = OI + OB = OI + 3 = \dfrac{11}{2}\)\( \Rightarrow P + \dfrac{25}{4}  \le \dfrac{121}{4} \Leftrightarrow P \le  24 \)