Câu hỏi:
1 năm trước
Đề thi THPT QG 2022 – mã đề 124
Trong không gian $O x y z$, cho điểm \(A(2;1; - 1)\). Gọi \((P)\) là mặt phẳng chứa trục $O y$ sao cho khoảng cách từ \(A\) đến \((P)\) lớn nhất. Phương trình của \((P)\) là:
Trả lời bởi giáo viên
Đáp án đúng: d
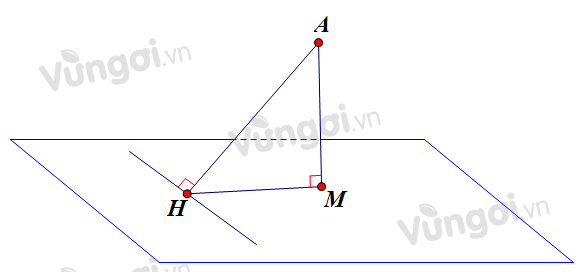
Gọi $H$ là hình chiếu của $A$ lên $Oy$.
Khi đó $H(0;1;0)$ và \(\overrightarrow {HA} = \left( {2;0;-1} \right)\)
Gọi M là hình chiếu của A lên mặt phẳng (P)
\( \Rightarrow AM \bot MH \Rightarrow AM \le AH\)\( \Rightarrow A{M_{\max }} = AH \Rightarrow AH \bot \left( P \right)\)
Mặt phẳng $(P): 2x-z=0$
Hướng dẫn giải:
- Gọi $H$ là hình chiếu của $A$ lên $Oy$.
- Gọi M là hình chiếu của A lên mặt phẳng (P)
- Chứng tỏ \(AM \le AH\)