Đề thi THPT QG 2022 – mã đề 124

Có bao nhiêu giá trị nguyên âm của tham số \(a\) để hàm số \(y = \left| {{x^4} + 2a{x^2} + 8x} \right|\) có đúng ba điểm cực trị?

Xét \(f(x) = {x^4} - m{x^2} - 64x\).

Ta có \(f'(x) = 4{x^3} + 4ax + 8 = 0\)\( \Rightarrow a =  - {x^2} - \dfrac{2}{x}\).

Đặt \(g(x) =  - {x^2} - \dfrac{2}{x} \)\(\Rightarrow g'(x) =  - 2x + \dfrac{2}{{{x^2}}}\) \( \Rightarrow g'(x) = 0 \Leftrightarrow x = 1\).

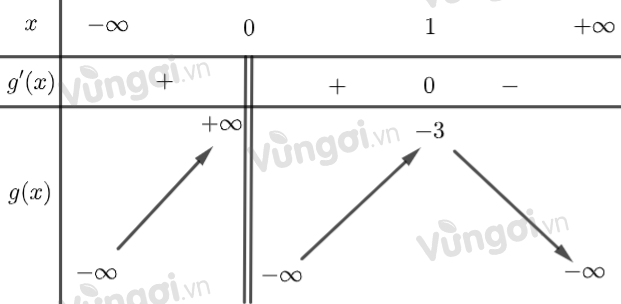
Từ bảng biến thiên ta thấy, đồ thị cắt đường thẳng $y=a$ tại 1 điểm nếu $a>-3$; cắt tại 2 điểm nếu $a=-3$; cắt tại 3 điểm nếu $a<-3$.

Khi đó:

+) Với $a>-3$=> Phương trình $f’(x)=0$ có 1 nghiệm lẻ khác 0

+) Với $a=-3$=> Phương trình $f’(x)=0$ có 2 nghiệm, trong đó 1 nghiệm lẻ, 1 nghiệm bội 2 đều khác 0.

+) Với $a<-3$=> Phương trình $f’(x)=0$ có 3 nghiệm lẻ khác 0.

Xét phương trình \(f(x) = 0 \Leftrightarrow {x^4} + 2a{x^2} + 8x = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^3} + 2ax + 8 = 0}\end{array}} \right.\).

=> $x=0$ luôn là một nghiệm lẻ của phương trình \(f(x) = 0\)

Xét \({x^3} + 2ax + 8 = 0 \Rightarrow a =  - \dfrac{{{x^2}}}{2} - \dfrac{4}{x}\).

Đặt \(h(x) =  - \dfrac{{{x^2}}}{2} - \dfrac{4}{x} \Rightarrow {h^\prime }(x) =  - x + \dfrac{4}{{{x^2}}}\) \( \Rightarrow {h^\prime }(x) = 0 \Leftrightarrow x = \sqrt[3]{4}\).

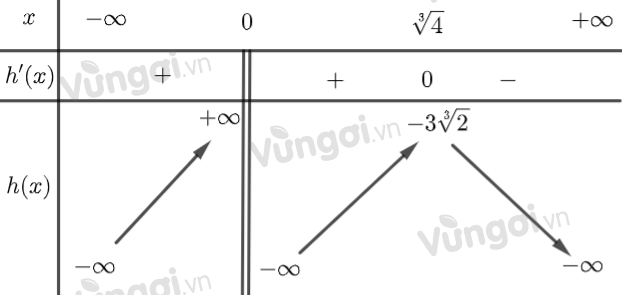
Từ bảng biến thiên ta thấy, đồ thị cắt đường thẳng $y=a$ tại 1 điểm nếu $a>-3\sqrt[3]{2}$; cắt tại 2 điểm nếu $ a=-3\sqrt[3]{2}$; cắt tại 3 điểm nếu $ a<-3\sqrt[3]{2}$.

Khi đó:

+) Với $ a>-3\sqrt[3]{2}$=> Phương trình $f’(x)=0$ có 1 nghiệm lẻ khác 0

+) Với $ a=-3\sqrt[3]{2}$=> Phương trình $f’(x)=0$ có 2 nghiệm, trong đó 1 nghiệm lẻ, 1 nghiệm bội 2 đều khác 0.

+) Với $ a<-3\sqrt[3]{2}$=> Phương trình $f’(x)=0$ có 3 nghiệm lẻ khác 0.

Ta có số điểm cực trị của hàm số \(y = |f(x)|\) bằng tổng số điểm cực trị của hàm số \(y = f(x)\) và số nghiệm bội lẻ của phương trình \(f(x) = 0\).

Vì $x=0$ luôn là một nghiệm lẻ của phương trình \(f(x) = 0\) nên số điểm cực trị của hàm số \(y = f(x)\) phải là 1.

=> Suy ra yêu cầu bài toán trở thành hàm số \(y = f(x)\) có 1 điểm cực trị và phương trình \(f(x) = 0\) có 2 nghiệm bội lẻ \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a \ge  - 3}\\{a \ge  - 3\sqrt[3]{2} \approx  - 3,78}\end{array} \Leftrightarrow a \ge  - 3} \right.\).

Vì \(a\) nguyên âm nên có 3 giá trị thỏa yêu cầu bài toán.