Đề thi THPT QG 2022 – mã đề 124
Cho khối lăng trụ đứng \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) có đáy $A B C$ là tam giác vuông cân tại \(A,AB = a\). Góc giữa đường thẳng \(B{C^\prime }\) và mặ̣t phẳng \(\left( {AC{C^\prime }{A^\prime }} \right)\) bằng \({30^o}\). Thể tích của khối lăng trụ đã cho bằng
Trả lời bởi giáo viên
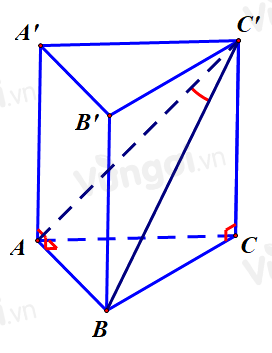
Ta có: \(AB \bot AC;AB \bot AA' \Rightarrow AB \bot \left( {ACC'A'} \right)\)
=> Góc giữa \(B{C^\prime }\) và mặ̣t phẳng \(\left( {AC{C^\prime }{A^\prime }} \right)\) là góc giữa BC’ và AC’ và bằng \(\widehat {BC'A} = {30^o}\)
Khi đó \(AC' = \sqrt 3 .AB = a\sqrt 3 \)
Mà \(AC = AB = a\)
\( \Rightarrow AA' = \sqrt {AC{'^2} - A{C^2}} = a\sqrt 2 \)
Thể tích của khối lăng trụ đã cho bằng
\(V = \dfrac{1}{2}{a^2}.a\sqrt 2 = \dfrac{{{a^3}\sqrt 2 }}{2}\)
Hướng dẫn giải:
- Xác định góc giữa \(B{C^\prime }\) và mặ̣t phẳng \(\left( {AC{C^\prime }{A^\prime }} \right)\)