Câu hỏi:
1 năm trước
Đề thi THPT QG 2022 – mã đề 122
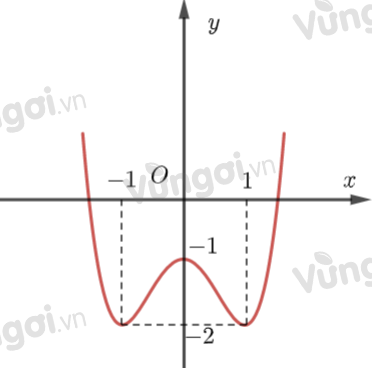
Cho hàm số $f(x)=ax^{4}+bx^{2}+c$ có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên thuộc đoạn $[-2 ; 5]$ của tham số $m$ để phương trình $f(x)=m$ có đúng 2 nghiệm thực phân biệt?
Trả lời bởi giáo viên
Đáp án đúng: b
Phương trình $f(x)=m$ có đúng 2 nghiệm thực phân biệt khi và chỉ khi đường thẳng $y=m$ cắt đồ thị hàm số $y=f(x)$ tại 2 điểm phân biệt.
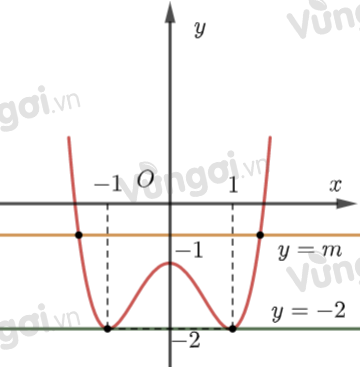
Từ đồ thị ta thấy đường thẳng y=m cắt đồ thị hàm số tại đúng 2 điểm phân biệt khi và chỉ khi:
\(\left[ \begin{array}{l}m > - 1\\m = - 2\end{array} \right. \Leftrightarrow m \in \left\{ { - 2;0;1;2;3;4;5} \right\}\)
Vậy có 7 giá trị $m$ thỏa mãn.
Hướng dẫn giải:
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y =M\)
Câu hỏi khác
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 101 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 102 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 103 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 104 có lời giải chi tiết
- Đề thi THPT QG chính thức - 2022 - mã đề 122 có lời giải chi tiết
