Đề thi THPT QG 2019 – mã đề 104

Cho phương trình \(\left( {2\log _3^2x - {{\log }_3}x - 1} \right)\sqrt {{4^x} - m}  = 0\) (m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt ?

ĐK: \(\left\{ \begin{array}{l}x > 0\\{4^x} - m \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 0\\x \ge {\log _4}m\,\,\left( {Do\,\,m > 0} \right)\end{array} \right.\).

\(\begin{array}{l}\left( {2\log _3^2x - {{\log }_3}x - 1} \right)\sqrt {{4^x} - m}  = 0 \Leftrightarrow \left[ \begin{array}{l}2\log _3^2x - {\log _3}x - 1 = 0\\{4^x} = m\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{\log _3}x = 1\\{\log _3}x =  - \dfrac{1}{2}\\{4^x} = m\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = \dfrac{1}{{\sqrt 3 }}\\{4^x} = m\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = \dfrac{1}{{\sqrt 3 }}\\x = {\log _4}m\end{array} \right.\end{array}\)

Biểu diễn các nghiệm trên trục số ta có:

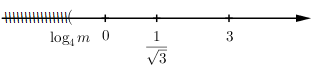
Phương trình có 2 nghiệm phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}{\log _4}m = 0\\\dfrac{1}{{\sqrt 3 }} \le {\log _4}m < 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 1\\2,26 \le m < 64\end{array} \right.\).

Lại có \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {1;3;4;5;...;63} \right\}\). Vậy có 62 giá trị của \(m\) thỏa mãn yêu cầu bài toán.