Đề thi THPT QG 2019 – mã đề 104

Cho đường thẳng \(y = \dfrac{3}{2}x\) và parabol \(y = {x^2} + a\)  (\(a\) là tham số thực dương). Gọi \({S_1}\) và \({S_2}\) lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên.

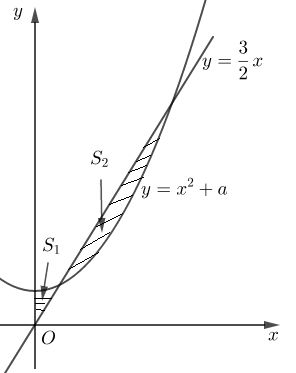
Khi \({S_1} = {S_2}\) thì \(a\) thuộc khoảng nào dưới đây ?

Xét phương trình hoành độ giao điểm \({x^2} + a = \dfrac{3}{2}x \Leftrightarrow 2{x^2} - 3x + 2a = 0\,\,\left( * \right)\).

Phương trình có 2 nghiệm phân biệt \( \Leftrightarrow \Delta  = 9 - 8a > 0 \Leftrightarrow a < \dfrac{9}{8}\).

Kết hợp điều kiện đề bài \( \Rightarrow 0 < a < \dfrac{9}{8}\).

Gọi \({x_1},\,\,{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) là 2 nghiệm của phương trình (*). Khi đó ta có:

\(\begin{array}{l}{S_1} = \int\limits_0^{{x_1}} {\left( {{x^2} + a - \dfrac{3}{2}x} \right)dx}  = \left. {\left( {\dfrac{{{x^3}}}{3} + ax - \dfrac{{3{x^2}}}{4}} \right)} \right|_0^{{x_1}} = \dfrac{{x_1^3}}{3} + a{x_1} - \dfrac{{3x_1^2}}{4}\\{S_2} = \int\limits_{{x_1}}^{{x_2}} {\left( {\dfrac{3}{2}x - {x^2} - a} \right)dx}  = \left. {\left( {\dfrac{{3{x^2}}}{4} - \dfrac{{{x^3}}}{3} - ax} \right)} \right|_{{x_1}}^{{x_2}} = \left( {\dfrac{{3x_2^2}}{4} - \dfrac{{x_2^3}}{3} - a{x_2}} \right) - \left( {\dfrac{{3x_1^2}}{4} - \dfrac{{x_1^3}}{3} - a{x_1}} \right)\end{array}\)

Theo bài ra ta có: \({S_1} = {S_2}\)

\(\begin{array}{l} \Leftrightarrow \dfrac{{x_1^3}}{3} + a{x_1} - \dfrac{{3x_1^2}}{4} = \left( {\dfrac{{3x_2^2}}{4} - \dfrac{{x_2^3}}{3} - a{x_2}} \right) - \left( {\dfrac{{3x_1^2}}{4} - \dfrac{{x_1^3}}{3} - a{x_1}} \right)\\ \Leftrightarrow \dfrac{{3x_2^2}}{4} - \dfrac{{x_2^3}}{3} - a{x_2} = 0 \Leftrightarrow 9x_2^2 - 4x_2^3 - 12a{x_2} = 0\\ \Leftrightarrow {x_2}\left( {4x_2^2 - 9{x_2} + 12a} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x_2} = 0\\4x_2^2 - 9{x_2} + 12a = 0\end{array} \right.\end{array}\)

TH1: \({x_2} = 0 \Rightarrow \) Thay vào (*) ta có \(2a = 0 \Leftrightarrow a = 0\,\,\left( {ktm} \right)\).

TH2: \(4x_2^2 - 9{x_2} + 12a = 0\) (1).   

Vì \({x_2}\) là nghiệm của (*) nên \(2x_2^2 - 3{x_2} + 2a = 0 \Leftrightarrow 12x_2^2 - 18{x_2} + 12a = 0\) (2).

Trừ vế theo vế của (2) cho (1) ta được \(8x_2^2 - 9{x_2} = 0 \Leftrightarrow \left[ \begin{array}{l}{x_2} = 0\\{x_2} = \dfrac{9}{8}\end{array} \right.\).

Với \({x_2} = 0 \Leftrightarrow 2a = 0 \Leftrightarrow a = 0\,\,\left( {ktm} \right)\).

Với \({x_2} = \dfrac{9}{8} \Leftrightarrow 2.{\left( {\dfrac{9}{8}} \right)^2} - 3.\dfrac{9}{8} + 2a = 0 \Leftrightarrow a = \dfrac{{27}}{{64}}\,\,\left( {tm} \right) = 0,421875\).

Vậy \(a \in \left( {\dfrac{2}{5};\dfrac{9}{{20}}} \right).\)