Đề thi THPT QG 2019 – mã đề 104

Trong không gian \(Oxyz\), cho điểm \(A\left( {0;3; - 2} \right)\). Xét đường thẳng \(d\) thay đổi, song song với trục \(Oz\) và cách trục \(Oz\) một khoảng bằng 2. Khi khoảng cách từ điểm \(A\) đến \(d\) lớn nhất, \(d\) đi qua điểm nào dưới đây ?

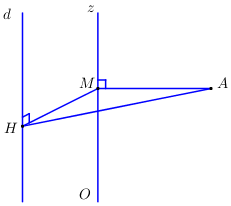
Gọi \({d_1}\) là khoảng cách từ \(A\) đến \(Oz\), \({d_2}\) là khoảng cách giữa \(Oz\) và \(d\).

Gọi \(M\) là hình chiếu của \(A\) trên \(Oz \Rightarrow M\left( {0;0; - 2} \right)\), ta có \(MA = 3 \Rightarrow d\left( {A;Oz} \right) = 3\).

Gọi \(H\) là hình chiếu của \(M\) trên \(d\) ta có \(HM \bot d\) và \(HM = 2\).

\(\left\{ \begin{array}{l}AM \bot Oz \Rightarrow AM \bot d\\HM \bot d\end{array} \right. \Rightarrow d \bot \left( {AMH} \right)\)\( \Rightarrow AH \bot d \Rightarrow d\left( {A;d} \right) = AH\).

Áp dụng định lí Cosin trong tam giác \(AHM\) ta có:

\(\begin{array}{l}\,\,\,\,\,\,A{H^2} = A{M^2} + H{M^2} - 2AM.HM.\cos \angle AMH\\ \Rightarrow A{H^2} = {3^2} + {2^2} - 2.3.2.\cos \angle AMH\\ \Rightarrow A{H^2} = 13 - 12\cos \angle AMH\end{array}\)

\( \Rightarrow A{H_{\max }} \Leftrightarrow A{H^2}_{\max } \Leftrightarrow \cos \angle AM{H_{\min }}\)

\( \Leftrightarrow \cos \angle AMH =  - 1 \Leftrightarrow \angle AMH = {180^0}\) hay \(A,\,\,M,\,\,H\) thằng hàng và \(M\) nằm giữa \(A\) và \(H\).

Khi đó ta có \(\dfrac{{AM}}{{HM}} = \dfrac{3}{2} \Rightarrow \overrightarrow {AM}  = \dfrac{3}{2}\overrightarrow {MH} \).

\( \Rightarrow \left( {0; - 3;0} \right) = \dfrac{3}{2}\left( {{x_H};{y_H};{z_H} - 2} \right)\)\( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{3}{2}{x_H} = 0\\\dfrac{3}{2}{y_H} =  - 3\\\dfrac{3}{2}{z_H} - 3 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_H} = 0\\{y_H} =  - 2\\{z_H} = 2\end{array} \right. \Rightarrow H\left( {0; - 2;2} \right)\)

\( \Rightarrow \) Phương trình đường thẳng \(d:\,\,\left\{ \begin{array}{l}x = 0\\y =  - 2\\z = 2 + t\end{array} \right.\).

Dựa vào các đáp án ta thấy chỉ có điểm \(P\left( {0; - 2; - 5} \right) \in d\).