Câu hỏi:
2 năm trước
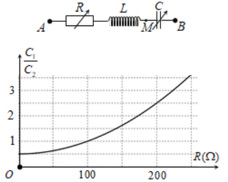
Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu đoạn mạch AB, trong đó R là biến trở, cuộn cảm thuần có hệ số tự cảm L, tụ điện có điện dung C thay đổi được. Khi \(C = {C_1}\) thì điện áp hai đầu đoạn mạch AM không phụ thuộc vào giá trị của R. Khi \(C = {C_2}\) thì điện áp hiệu dụng giữa hai đầu đoanh mạch MB đạt giá trị cực đại. Hình bên là đồ thị biểu diễn sự phụ thuộc của tỉ số \(\dfrac{{{C_1}}}{{{C_2}}}\) theo R. Giá trị của cảm kháng \({Z_L}\) là
Trả lời bởi giáo viên
Đáp án đúng: c
+ Khi \(C = {C_1}\): \({U_{RL}}\) không phụ thuộc vào R khi đó: \({Z_{{C_1}}} = 2{Z_L}\)
+ Khi \(C = {C_2}\): \({U_{{C_{max}}}}\) khi đó \({Z_{C2}} = \dfrac{{{R^2} + Z_L^2}}{{{Z_L}}}\)
Xét tỉ số: \(\dfrac{{{C_1}}}{{{C_2}}} = \dfrac{{{Z_{{C_2}}}}}{{{Z_{{C_1}}}}} = \dfrac{{{R^2} + Z_L^2}}{{2Z_L^2}}\) (*)
Từ đồ thị, tại điểm \(\dfrac{{{C_1}}}{{{C_2}}} = 1\) ta có \(R = 100\Omega \)
Thay vào (*) suy ra \({Z_L} = 100\Omega \)
Hướng dẫn giải:
Vận dụng các bài toán C biến thiên
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
