Trả lời bởi giáo viên
Đáp án đúng: d
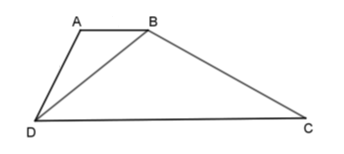
Vì ΔABD∽ (gt) nên \widehat {ABD} = \widehat {BDC} (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AB\,{\rm{//}}\,CD suy ra ABCD là hình thang (dấu hiệu nhận biết) hay B đúng.
Lại có \Delta ABD\backsim\Delta BDC nên \dfrac{{AB}}{{BD}} = \dfrac{{AD}}{{BC}} (cạnh tương ứng) nên A đúng.
\Delta ABD\backsim\Delta BDC \Rightarrow \dfrac{{AB}}{{BD}} = \dfrac{{BD}}{{DC}} (cạnh tương ứng) \Rightarrow AB.CD = B{D^2} hay C đúng.
Chỉ có D sai.
Hướng dẫn giải:
+ Sử dụng các góc tương ứng bằng nhau của hai tam giác đồng dạng để chứng minh cặp góc so le trong bằng nhau.
+ Từ đó suy ra cặp cạnh song song và suy ra ABCD là hình thang.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
