Trả lời bởi giáo viên
Đáp án đúng: d
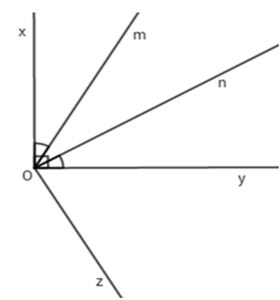
Vì $Oy$ là tia phân giác của góc $mOz$ nên \(\widehat {mOz} = 2.\widehat {mOy} = {2.60^0} = {120^0}\)
Trên nửa mặt phẳng bờ chứa tia $Om$ có: \(\widehat {mOn} < \widehat {mOz}\,\,\left( {{{30}^0} < {{120}^0}} \right)\)
Suy ra tia $On$ nằm giữa hai tia $Om$ và $Oz$
$ \Rightarrow \widehat {mOn} + \widehat {nOz} = \widehat {mOz} \Rightarrow {30^0} + \widehat {nOz} = {120^0}$
$ \Rightarrow \widehat {nOz} = {120^0} - {30^0} = {90^0}$
Vậy $On$ vuông góc với $Oz.$
Hướng dẫn giải:
Áp dụng tính chất tia nằm giữa hai tia còn lại. Từ đó áp dụng công thức cộng góc, tính số đo góc $nOz.$ Từ đó chứng minh $On$ vuông góc với $Oz.$
Câu hỏi khác
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
