Câu hỏi:
3 năm trước
Cho tứ diện \(ABCD\) có \(AB \bot CD\) và \(AC \bot BD\). Gọi \(H\) là hình chiếu vuông góc của \(A\) lên \(mp(BCD)\). Các khẳng định sau, khẳng định nào sai?
Trả lời bởi giáo viên
Đáp án đúng: d
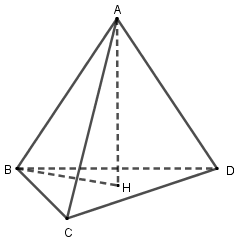
Ta có \(\left\{ \begin{array}{l}CD \bot AB\\CD \bot AH\end{array} \right. \Rightarrow CD \bot (ABH) \Rightarrow CD \bot BH\). Tương tự \(BD \bot CH\)
Suy ra \(H\) là trực tâm \(\Delta BCD\). Suy ra đáp án A, B đúng.
Ta có \(\left\{ \begin{array}{l}BC \bot AH\\BC \bot DH\end{array} \right. \Rightarrow BC \bot AD\), suy ra C đúng.

