Câu hỏi:
2 năm trước
Cho tam giác vuông \(ABC\) vuông tại \(A\) có \(BC = 20\,cm;AC = 12\,cm\) . Quay tam giác \(ABC\) cạnh \(AB\) ta được một hình nón có thể tích là :
Trả lời bởi giáo viên
Đáp án đúng: d
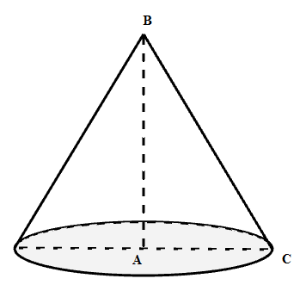
Khi quay tam giác \(ABC\) quanh cạnh \(AB\) ta được một hình nón có chiều cao \(AB\) và bán kính đường tròn đáy là cạnh \(AC\) .
Theo định lý Pytago ta có \(A{B^2} = B{C^2} - A{C^2} = {20^2} - {12^2} \Rightarrow AB = 16\)
Thể tích của khối nón là \(V = \dfrac{1}{3}\pi A{C^2}AB = \dfrac{1}{3}\pi {.12^2}.16 = 768\pi \,\,\left( {c{m^3}} \right)\)
Hướng dẫn giải:
Sử dụng công thức tính thể tích khối nón $V = \dfrac{1}{3}\pi {R^2}h$

