Trả lời bởi giáo viên
Đáp án đúng: a
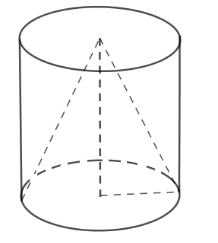
Ta thấy hình nón có bán kính đáy bằng bán kính đáy hình trụ và chiều cao bằng chiều cao hình trụ nên
\({V_t} = \pi {R^2}h\) và \({V_n} = \dfrac{1}{3}\pi {R^2}h \Rightarrow {V_t} = 3{V_n}\) . Do đó phần gỗ bỏ đi chiếm \(\dfrac{2}{3}\) thể tích khối trụ
Nên thể tích khối trụ là \({V_t} = 640\pi :\dfrac{2}{3} = 960\pi \,\,\left( {c{m^3}} \right)\) .
Hướng dẫn giải:
Sử dụng công thức tính thể tích khối trụ \(V = \pi {R^2}h\) và thể tích khối nón \(V = \dfrac{1}{3}{R^2}h\) để suy ra mối quan hệ giữa thể tích hai khối và phần gỗ bỏ đi.

