Câu hỏi:
2 năm trước
Cho tam giác đều \(ABC\) cạnh bằng \(2cm.\) Tính bán kính \(R\) của đường tròn ngoại tiếp tam giác \(ABC.\)
Trả lời bởi giáo viên
Đáp án đúng: c
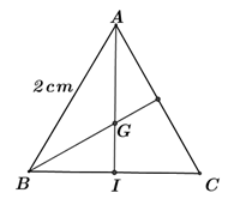
Gọi \(I\) là trung điểm của \(BC,\,\,G\) là trọng tâm tam giác \(ABC\) và \(R\) là bán kính đường tròn ngoại tiếp tam giác \(ABC\) thì \(R = AG = \dfrac{2}{3}.AI\)
Trong tam giác \(ABI\) vuông tại \(I\) có:
\(A{I^2} = A{B^2} - I{B^2} = {2^2} - 1 = 3 \Rightarrow AI = \sqrt 3 \,\,\,\left( {cm} \right).\)
Khi đó: \(R = \dfrac{2}{3}AI = \dfrac{{2\sqrt 3 }}{3}cm.\)
Hướng dẫn giải:
Tam giác đều thì tâm đường tròn ngoại tiếp tam giác trùng với trọng tâm, từ đó áp dụng định lý Pytago.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
