Cho tam giác \(ABC\) vuông tại \(A\) , đường cao \(AH\) . Biết \(AB = 10cm;\,AH = 6cm\). Tính độ dài các cạnh \(AC,BC\) của tam giác \(ABC\). 

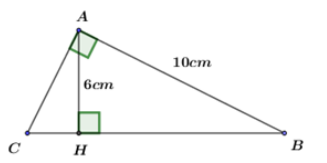
Áp dụng định lý Py-ta-go cho tam giác \(ABH\) vuông tại H. Ta có:

\(\begin{array}{l}A{H^2} + B{H^2} = A{B^2}\\ \Rightarrow B{H^2} = A{B^2} - A{H^2} = {10^2} - {6^2} = 100 - 36 = 64\\ \Rightarrow B{H^2} = {8^2}\\ \Rightarrow BH = 8\,\left( {cm} \right)\end{array}\)

Trong tam giác vuông \(ABC\) vuông tại \(A\) có AH là đường cao

\(\begin{array}{l} \Rightarrow A{B^2} = BH.BC\\ \Rightarrow BC = \dfrac{{A{B^2}}}{{BH}} = \dfrac{{{{10}^2}}}{8} = \dfrac{{100}}{8} = 12,5\,\left( {cm} \right)\end{array}\)

Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:

\(\begin{array}{l}A{C^2} = B{C^2} - A{B^2} = 12,{5^2} - {10^2} = 56,25\\ \Rightarrow AC = 7,5\,\,\,\,\left( {cm} \right).\end{array}\)

Vậy: \(AC = 7,5\,\left( {cm} \right);\,\,\,\,BC = 12,5\,\left( {cm} \right).\)