Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 6, AC = 8\). Tia phân giác góc \(B\) cắt \(AC\) tại \(D\). Độ dài \(AD\) là:
Trả lời bởi giáo viên
Đáp án đúng: b
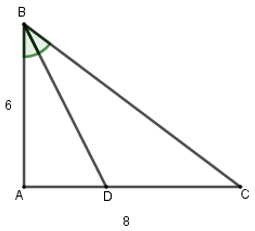
Tam giác \(ABC\) vuông tại \(A\), áp dụng định lý Pi-ta-go có:
\(B{C^2} = A{B^2} + A{C^2}\) \( = {6^2} + {8^2} = 100\) \( \Rightarrow BC = 10\).
\(BD\) là tia phân giác góc \(B\) nên \(\dfrac{{DA}}{{DC}} = \dfrac{{BA}}{{BC}} = \dfrac{6}{{10}} = \dfrac{3}{5}\) \( \Rightarrow \dfrac{{DA}}{3} = \dfrac{{DC}}{5}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{{DA}}{3} = \dfrac{{DC}}{5}\)\( = \dfrac{{DA + DC}}{{3 + 5}} = \dfrac{{AC}}{8} = \dfrac{8}{8} = 1\)
\( \Rightarrow DA = 3.1 = 3; DC = 5.1 = 5\).
Vậy \(AD = 3\).
Hướng dẫn giải:
- Sử dụng định lí Pi-ta-go tính \(BC\).
- Sử dụng tính chất đường phân giác của tam giác tính \(AD\).
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
