Trả lời bởi giáo viên
Đáp án đúng: a
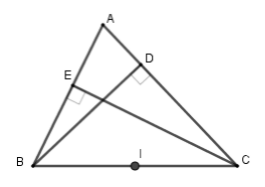
Gọi \(I\) là trung điểm của \(BC\).
Xét tam giác \(BEC\) vuông tại \(E\) có \(EI = IB = IC = \dfrac{{BC}}{2}\) (vì \(EI\) là đường trung tuyến ứng với cạnh huyền)
Xét tam giác \(BDC\) vuông tại \(D\) có \(DI = IB = IC = \dfrac{{BC}}{2}\) (vì \(DI\) là đường trung tuyến ứng với cạnh huyền)
Từ đó ta có \(ID = IE = IB = IC = \dfrac{{BC}}{2}\) nên bốn điểm \(B,E,D,C\) cùng nằm trên một đường tròn có bán kính \(R = \dfrac{{BC}}{2}\).
Ta thấy \(IA > ID\) nên điểm \(A\) không thuộc đường tròn trên.
Hướng dẫn giải:
Sử dụng: Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
