Cho tam giác \(ABC\) có: \(AB = 4cm, AC = 5cm, BC = 6cm\). Các đường phân giác \(BD\) và \(CE\) cắt nhau ở \(I\). Tỉ số diện tích các tam giác \(DIE\) và \(ABC\) là:

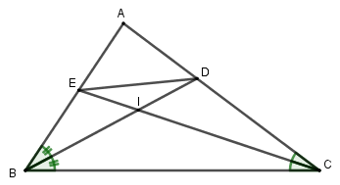
Ta có: \(\dfrac{{AD}}{{AB}} = \dfrac{{DC}}{{BC}}\) (t/c)\( \Rightarrow \dfrac{{AD}}{4} = \dfrac{{DC}}{6} = \dfrac{{AD + DC}}{{4 + 6}} = \dfrac{5}{{10}} = \dfrac{1}{2}\)

\( \Rightarrow AD = 4.\dfrac{1}{2} = 2,DC = 6.\dfrac{1}{2} = 3\).

Suy ra

\(\dfrac{{DI}}{{IB}} = \dfrac{{DC}}{{CB}} = \dfrac{3}{6} = \dfrac{1}{2} \Rightarrow \dfrac{{DI}}{{DB}} = \dfrac{1}{3}\);

\(\dfrac{{BE}}{{EA}} = \dfrac{{BC}}{{AC}} = \dfrac{6}{5} \Rightarrow \dfrac{{BE}}{{BA}} = \dfrac{6}{{11}}\);

\(\dfrac{{AD}}{{DC}} = \dfrac{2}{3} \Rightarrow \dfrac{{AD}}{{AC}} = \dfrac{2}{5}\).

Suy ra \({S_{DIE}} = \dfrac{1}{3}{S_{BDE}},\) \({S_{DBE}} = \dfrac{6}{{11}}{S_{ABD}},\) \({S_{ABD}} = \dfrac{2}{5}{S_{ABC}}\)

\( \Rightarrow {S_{DIE}} = \dfrac{1}{3}.\dfrac{6}{{11}}.\dfrac{2}{5} = \dfrac{4}{{55}}{S_{ABC}}\).

Vậy \(\dfrac{{{S_{DIE}}}}{{{S_{ABC}}}} = \dfrac{4}{{55}}\).