Câu hỏi:
2 năm trước
Cho tam giác $ABC$ cân tại $A$. Gọi $D,E$ theo thứ tự thuộc các cạnh bên $AB,AC$ sao cho $AD{\rm{ }} = {\rm{ }}AE$ .
Tính các góc của hình thang $BDEC$ , biết $\widehat A = {70^o}$ .
Trả lời bởi giáo viên
Đáp án đúng: a
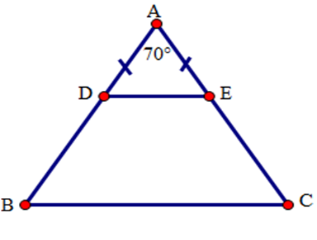
Ta có : \(\hat A = 70^\circ \)
Theo ý a) suy ra:
\(\widehat {ADE} = \widehat {AED} = \widehat {ABC} = \widehat {ACB} = \left( {180^\circ - \widehat {DAE}} \right):2\;\)\( = (180^\circ - 70^\circ ):2 = 55^\circ \;\;\;\;\;\;\)
Vì \(\widehat {BDE}\) và \(\widehat {ADE}\) là hai góc kề bù nên \(\widehat {BDE} = 180^\circ - \widehat {ADE} = 180^\circ - 55^\circ = 125^\circ \)$ \Rightarrow \widehat {DEC} = 125^\circ $ (Vì $DEBC$ là hình thang cân)
Vậy \(\widehat {BDE} = \widehat {DEC} = 125^\circ ;\,\widehat {DBC} = \widehat {ECB} = 55^\circ \) .
Hướng dẫn giải:
Ta sử dụng định lý về tổng các góc trong tam giác và tính chất về góc của hình thang cân.
