Câu hỏi:
2 năm trước
Cho tam giác $ABC$. Các tia phân giác của các góc \(B\) và \(C\) cắt nhau tại \(I\). Qua \(I\) kẻ đường thẳng song song với $BC$, cắt các cạnh $AB,AC$ lần lượt tại $D$ và $E$.
Chọn khẳng định đúng nhất?
Trả lời bởi giáo viên
Đáp án đúng: d
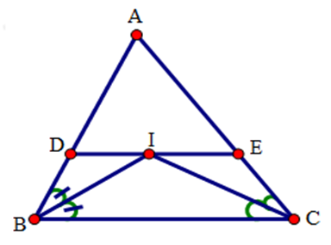
Xét tứ giác $DECB$ có: $DE//BC$ (gt) nên tứ giác $DECB$ là hình thang.
Tương tự :
Tứ giác $DICBS$ có $DI//BC$ (gt) nên tứ giác $DICB$ là hình thang
Tứ giác $IECB$ có $IE//CB$ (gt) nên tứ giác $IECB$ là hình thang.
Hướng dẫn giải:
Ta sử dụng định nghĩa hình thang: Tứ giác có hai cạnh đối song song là hình thang.
Giải thích thêm:
Một số em khi chứng minh được $DECB$ là hình thang thì chọn luôn đáp án A là sai.

