Câu hỏi:
2 năm trước
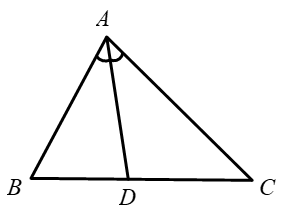
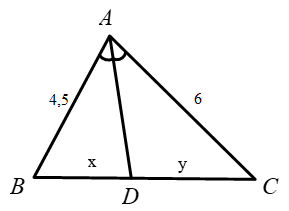
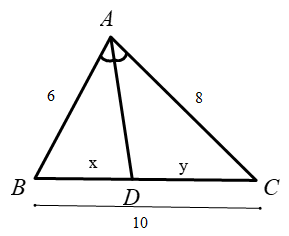
Cho tam giác \(ABC\), \(AC = 2AB\), \(AD\) là đường phân giác của tam giác\(ABC\). Xét các khẳng định sau, số khẳng định đúng là:
(I) \(\dfrac{{BD}}{{DC}} = \dfrac{1}{2}\) (II) \(\dfrac{{DC}}{{BC}} = \dfrac{2}{3}\) (III) \(\dfrac{{BD}}{{BC}} = \dfrac{1}{2}\)
Trả lời bởi giáo viên
Đáp án đúng: d
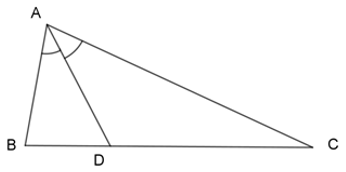
Vì \(AD\) là phân giác của \(\Delta ABC\) nên: \(\dfrac{{AB}}{{AC}} = \dfrac{{BD}}{{DC}}\)
Theo bài, ta có: \(AC = 2AB\)
\( \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{1}{2} \Rightarrow \dfrac{{BD}}{{DC}} = \dfrac{1}{2}\) hay (I) đúng.
Lại có \(\dfrac{{BD}}{{DC}} = \dfrac{1}{2}\) \( \Rightarrow \dfrac{{BD}}{{BC}} = \dfrac{{BD}}{{DC + BD}} = \dfrac{1}{{2 + 1}} = \dfrac{1}{3}\) nên (III) sai.
\( \Rightarrow \dfrac{{DC}}{{BC}} = \dfrac{{BC - BD}}{{BC}}\) \( = 1 - \dfrac{{BD}}{{BC}} = 1 - \dfrac{1}{3} = \dfrac{2}{3}\) hay (II) đúng.
Vậy chỉ có \(2\) khẳng định đúng.
Hướng dẫn giải:
Áp dụng tính chất đường phân giác của tam giác để tìm ra tỉ lệ thức phù hợp, từ đó tìm ra kết quả của đề bài.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
