Cho tam giác \(ABC,\) \(AB = AC = 10cm, BC = 12cm\). Gọi \(I\) là giao điểm của các đường phân giác của tam giác \(ABC\). Độ dài \(AI\) là:

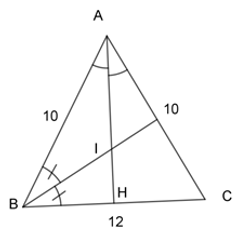
- Ta có \(AB = AC = 10 cm\)

Suy ra, \(\Delta ABC\) cân tại \(A\).

- Có \(I\) là giao các đường phân giác của \(\Delta ABC\).

Suy ra, \(AI, BI\) là đường phân giác của \(\Delta ABC\)

- Gọi \(H\) là giao của \(AI\) và \(BC\).

- Khi đó ta có \(AH\) vừa là đường phân giác, vừa là đường cao, vừa là đường trung tuyến ứng với cạnh đáy của tam giác cân \(ABC\) (tính chất tam giác cân).

\( \Rightarrow \) \(H\) là trung điểm của cạnh \(BC\) \( \Rightarrow BH = HC = \dfrac{{BC}}{2} = \dfrac{{12}}{2} = 6\;cm\).

Áp dụng định lý Pitago trong tam giác \(ABH\) vuông tại \(H\), ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,A{H^2} + B{H^2} = A{B^2}\\ \Leftrightarrow A{H^2} + {6^2} = {10^2}\\ \Leftrightarrow A{H^2} = 100 - 36 = 64\\ \Rightarrow AH = 8\end{array}\)

Vì \(BI\) là phân giác của tam giác \(ABH\) nên:

\(\dfrac{{AI}}{{IH}} = \dfrac{{AB}}{{BH}} = \dfrac{{10}}{6} = \dfrac{5}{3}\) \( \Rightarrow \dfrac{{AI}}{5} = \dfrac{{IH}}{3}\).

Theo tính chất dãy tỉ số bằng nhau ta có: \(\dfrac{{AI}}{5} = \dfrac{{IH}}{3} = \dfrac{{AI + IH}}{{5 + 3}}\) \( = \dfrac{{AH}}{8} = \dfrac{8}{8} = 1\)

\( \Rightarrow AI = 5\left( {cm} \right)\).