Cho tam giác \(ABC\), \(\widehat A = {90^0}\), \(AB = 15 cm, AC = 20 cm\), đường cao \(AH\)\((H \in BC)\). Tia phân giác của \(\widehat {HAB}\) cắt \(HB\) tại \(D\). Tia phân giác của \(\widehat {HAC}\) cắt \(HC\) tại \(E\). Tính \(HE\)?

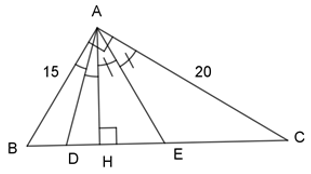
Áp dụng định lý Pytago vào tam giác \(ABC\) vuông tại \(A\), ta có:

\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Leftrightarrow {15^2} + {20^2} = B{C^2}\\ \Rightarrow BC = 25\end{array}\).

Ta có: \({S_{\Delta ABC}} = \dfrac{1}{2}.AB.AC = \dfrac{1}{2}.AH.BC\)

\( \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{15.20}}{{25}} = 12\)

Áp dụng định lý Pitago trong tam giác \(AHB\) vuông tại \(H\), ta có:

\(\begin{array}{l}\,\,\,\,\,\,A{B^2} = A{H^2} + H{B^2}\\ \Leftrightarrow {15^2} = {12^2} + H{B^2}\\ \Rightarrow H{B^2} = 81 \Rightarrow HB = 9\\ \Rightarrow HC = BC - HB = 25 - 9 = 16.\end{array}\)

Vì \(AE\) là phân giác của tam giác \(CAH\) nên:

\(\dfrac{{AC}}{{AH}} = \dfrac{{CE}}{{EH}} \Leftrightarrow \dfrac{{AC}}{{AH}} = \dfrac{{CH - EH}}{{EH}}\)\( \Leftrightarrow \dfrac{{20}}{{12}} = \dfrac{{16 - HE}}{{HE}}\)\( \Leftrightarrow 20HE = 12\left( {16 - HE} \right)\) \( \Leftrightarrow 20HE + 12HE = 12.16\)

\( \Leftrightarrow 32HE = 192 \Leftrightarrow HE = 6\left( {cm} \right)\).