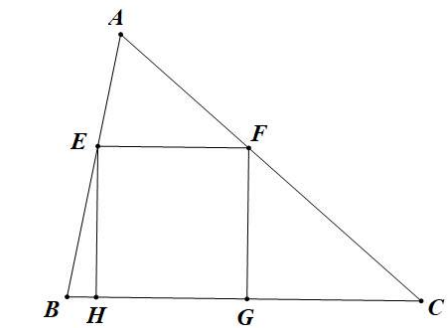
Cho tam giác $A B C$ có \(AB = 2a,AC = 3a,\widehat {BAC} = {60^o}\). Tính diện tích hình vuông $E F G H$ có $H, G$ nằm trên cạnh $B C, E$ nằm trên cạnh $A B$ và \(F\) nằm trên cạnh $A C$.
Trả lời bởi giáo viên
\(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos {60^o}\)\( = 7{a^2}\)\( \Rightarrow BC = a\sqrt 7 \)
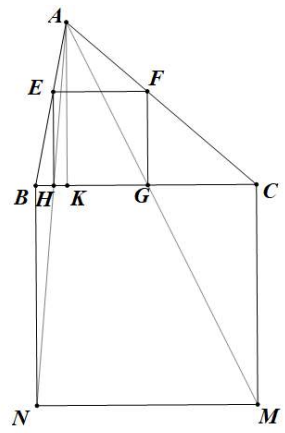
Dựng hình vuông BCMN như hình vẽ. Khi đó phép vị tự \({V_{\left( {A,\dfrac{{AB}}{{AE}}} \right)}}\) biến hình vuông EFGH thành hình vuông BCMN. Do đó \({S_{EFGH}} = {\left( {\dfrac{{AE}}{{AB}}} \right)^2}.{S_{BCMN}}\)
Gọi K là chân đường cao kẻ từ A lên BC, ta có: \(AK = \dfrac{{AB.AC.\sin {{60}^o}}}{{BC}} = \dfrac{{3\sqrt {21} }}{7}\)
Ta có:
\(\dfrac{{AH}}{{HN}} = \dfrac{{AK}}{{BK}} = \dfrac{{3\sqrt 3 }}{7}\)\( \Rightarrow \dfrac{{AH}}{{AN}} = \dfrac{{3\sqrt 3 }}{{3\sqrt 3 + 7}}\)\( \Rightarrow \dfrac{{AE}}{{AB}} = \dfrac{{3\sqrt 3 }}{{3\sqrt 3 + 7}}\)
Vậy \({S_{EFGH}} = {\left( {\dfrac{{3\sqrt 3 }}{{3\sqrt 3 + 7}}} \right)^2}.7{a^2} = \dfrac{{189{a^2}}}{{76 + 42\sqrt 3 }}\)
Hướng dẫn giải:
- Tính BC dựa vào định lý cos.
- Dựng hình vuông BCMN
- Xác định ảnh của phép vị tự \({V_{\left( {A,\dfrac{{AB}}{{AE}}} \right)}}\) biến hình vuông EFGH và biểu diễn diện tích của EFGH theo diện tích của BCMN
- Gọi K là chân đường cao kẻ từ A lên BC
- Tính \(\dfrac{{AE}}{{AB}}\)
Câu hỏi khác
- Đề thi thử phần Toán ĐGTD Đại học Bách Khoa Hà Nội lần 1, có đáp án và lời giải chi tiết
- Đề thi thử phần Toán ĐGTD Đại học Bách Khoa Hà Nội lần 2, có đáp án và lời giải chi tiết
- Đề thi chính thức ĐGTD Bách khoa 2022 - mã 103 có đáp án và lời giải chi tiết
- Đề thi thử ĐGTD Bách khoa trường Yên Lạc - Lần 2 có đáp án và lời giải chi tiết
