Cho phương trình \(\cos 3x = 1\). Tính diện tích đa giác có các đỉnh là các điểm biểu diễn họ nghiệm của phương trình đã cho trên đường tròn lượng giác.
Trả lời bởi giáo viên
\(\cos 3x = 1 \Leftrightarrow 3x = k2\pi \Leftrightarrow x = \dfrac{{k2\pi }}{3}\)
Với
\(\begin{array}{l}k = 0 \Rightarrow x = 0 \Rightarrow {M_1}\\k = 1 \Rightarrow x = \dfrac{{2\pi }}{3} \Rightarrow {M_2}\\k = 2 \Rightarrow x = \dfrac{{4\pi }}{3} \Rightarrow {M_3}\end{array}\)
Biểu diễn trên đường tròn:
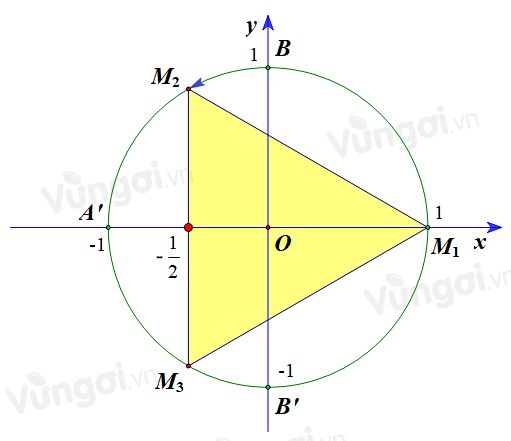
Tam giác \({M_1}{M_2}{M_3}\) là tam giác đều có cạnh \({M_2}{M_3} = \dfrac{{2\sqrt 3 }}{2} = \sqrt 3 \) và chiều cao \(k = 1 + \dfrac{1}{2} = \dfrac{3}{2}\)
Diện tích tam giác là \(S = \dfrac{1}{2}.\dfrac{3}{2}.\sqrt 3 = \dfrac{{3\sqrt 3 }}{4}\)
Hướng dẫn giải:
- Giải phương trình tìm các điểm biểu diễn
- Biểu diễn trên đường tròn và tính diện tích.