Câu hỏi:
2 năm trước
Cho nửa đường tròn $\left( O \right)$, đường kính $AB$ và một dây $CD$. Kẻ $AE$ và $BF$ vuông góc với $CD$ lần lượt tại $E$ và $F$ . So sánh độ dài $CE$ và $DF$ .
Trả lời bởi giáo viên
Đáp án đúng: d
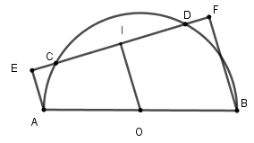
Lấy $I$ là trung điểm của $EF$
Xét tứ giác $AEFB$ có $AE\,{\rm{//}}FB$ (vì cùng vuông với $EF$) nên $AEFB$ là hình thang vuông tại $E;F$.
Ta có $OI$ là đường trung bình của hình thang $AEFB$ nên $OI\,{\rm{//}}\,AE{\rm{//}}FB$$ \Rightarrow OI \bot EF$
Hay $OI \bot CD$ nên $I$ là trung điểm của $CD$ ( quan hệ giữa dây và đường kính)
Ta có $IE = IF;IC = ID \Rightarrow IE - IC = IF - ID \Leftrightarrow EC = DF$.
Hướng dẫn giải:
Bước 1: Lấy $I$ là trung điểm của $EF$
Bước 2: Sử dụng mối liên hệ giữa đường kính và dây của đường tròn để hoàn thành.

