Câu hỏi:
2 năm trước
Cho hai đường tròn \(\left( {O;6\,cm} \right)\) và \(\left( {O';2\,cm} \right)\) cắt nhau tại \(A,B\) sao cho \(OA\) là tiếp tuyến của \(\left( {O'} \right)\). Độ dài dây \(AB\) là
Trả lời bởi giáo viên
Đáp án đúng: b
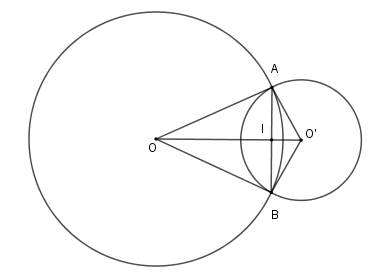
Vì \(OA\) là tiếp tuyến của \(\left( {O'} \right)\) nên \(\Delta OAO'\) vuông tại \(A\).
Vì \(\left( O \right)\) và \(\left( {O'} \right)\) cắt nhau tại \(A,B\) nên đường nối tâm \(OO'\) là trung trực của đoạn \(AB\).
Gọi giao điểm của \(AB\) và \(OO'\) là \(I\) thì \(AB \bot OO'\) tại \(I\) là trung điểm của \(AB\)
Áp dụng hệ thức lượng trong tam giác vuông \(OAO'\) ta có
\(\dfrac{1}{{A{I^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O'{A^2}}} = \dfrac{1}{{{6^2}}} + \dfrac{1}{{{2^2}}} \Rightarrow AI = \dfrac{{3\sqrt {10} }}{5}\,cm \Rightarrow AB = \dfrac{{6\sqrt {10} }}{5}\,cm\)
Hướng dẫn giải:
Sử dụng tính chất đường nối tâm của hai đường tròn cắt nhau và hệ thức lượng trong tam giác vuông.
