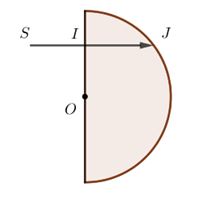
Cho một khối thủy tinh dạng bán cầu có bán kính R, chiết suất \(n{\rm{ }} = {\rm{ }}1,5\) . Chiếu thẳng góc tới mặt phẳng của bán cầu một tia sáng SI. Biết điểm tới I cách tâm O của khối bán cầu đoạn \(\dfrac{2}{{3\sqrt 3 }}R\). Tia ló ra khỏi bán cầu lệch với phương OJ một góc bằng bao nhiêu?
Trả lời bởi giáo viên
Ta có: tia sáng đi thẳng qua mặt phẳng AB của khối bán cầu, tới mặt cầu tại J với góc tới là i
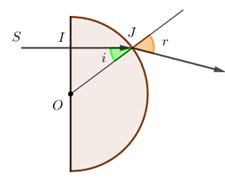
Từ hình ta có: \(\sin i = \dfrac{{OI}}{{OJ}} = \dfrac{{\dfrac{2}{{3\sqrt 3 }}R}}{R} = \dfrac{2}{{3\sqrt 3 }}\)
Mặt khác, theo định luật khúc xạ ánh sáng, ta có:
\(\begin{array}{l}n\sin i = {\mathop{\rm s}\nolimits} {\rm{inr}}\\ \Leftrightarrow 1,5.\dfrac{2}{{3\sqrt 3 }} = {\mathop{\rm s}\nolimits} {\rm{inr}}\\ \Rightarrow r = {35,26^0}\end{array}\)
Hướng dẫn giải:
+ Vẽ đường truyền tia sáng qua lưỡng chất phẳng
+ Sử dụng hệ thức lượng trong tam giác
+ Vận dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)

