Câu hỏi:
2 năm trước
Cho một hình quạt tròn có bán kính \(12\,cm\) và góc ở tâm là \({135^o}\) . Người ta uốn hình quạt này thành một hình nón. Tính thể tích của khối nón đó.
Trả lời bởi giáo viên
Đáp án đúng: c
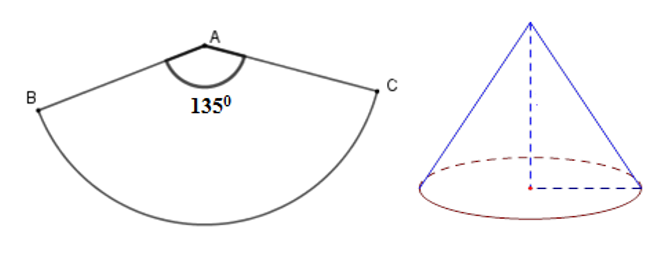
Ta uốn hình quạt \(BAC\) thành hình nón đỉnh \(A\) , đường sinh \(AB = 12\,cm\) .
Khi đó độ dài cung \(BC\) chính là chu vi đáy của hình nón
Ta có độ dài cung \(BC\) là \({l_{BC}} = \dfrac{{\pi .12.135}}{{180}} = 9\pi \)
Khi đó chu vi đáy của hình nón \(C = 2\pi R = 9\pi \Rightarrow R = 4,5\,cm\)\( \Rightarrow {h^2} = {l^2} - {R^2} = {12^2} - 4,{5^2} \Rightarrow h = \dfrac{{3\sqrt {55} }}{2}\,cm\)
Thể tích khối nón \(V = \dfrac{1}{3}\pi .4,{5^2}.\dfrac{{3\sqrt {55} }}{2} = \dfrac{{41\pi \sqrt {55} }}{8}\) \(\left( {c{m^3}} \right)\)
Hướng dẫn giải:
Sử dụng công thức thể tích khối nón \(V = \dfrac{1}{3}\pi {R^2}h\)
Độ dài cung tròn bán kính \(R\) và số đo cung \(n^\circ \) là \(l = \dfrac{{\pi Rn}}{{180}}\)
