Câu hỏi:
2 năm trước
Cho mạch điện như hình vẽ:
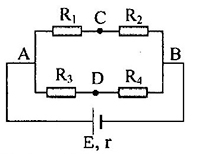
\(E = 12V\), \(r = 1\Omega \),\({R_1} = {R_2} = 4\Omega \), \({R_3} = 3\Omega \), \({R_4} = 5\Omega \). Tìm hiệu điện thế giữa hai đầu AB \(\left( {{U_{AB}}} \right)\)?
Trả lời bởi giáo viên
Đáp án đúng: b
+ Ta có mạch gồm: \(\left[ {{R_1}nt{R_2}} \right]//\left[ {{R_3}nt{R_4}} \right]\)
\(\left\{ \begin{array}{l}{R_{12}} = {R_1} + {R_2} = 4 + 4 = 8\Omega \\{R_{34}} = {R_3} + {R_4} = 3 + 5 = 8\Omega \end{array} \right.\)
Điện trở tương đương của mạch ngoài: \({R_N} = \dfrac{{{R_{12}}{R_{23}}}}{{{R_{12}} + {R_{23}}}} = \dfrac{{8.8}}{{8 + 8}} = 4\Omega \)
+ Cường độ dòng điện trong mạch chính: \(I = \dfrac{E}{{{R_N} + r}} = \dfrac{{12}}{{4 + 1}} = 2,4A\)
+ Hiệu điện thế giữa hai điểm A, B: \({U_{AB}} = I.{R_N} = 2,4.4 = 9,6V\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính điện trở tương đương của các điện trở mắc nối tiếp: \(R = {R_1} + {R_2} + ...\)
+ Sử dụng biểu thức tính điện trở tương đương của các điện trở mắc song song: \(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ...\)
+ Sử dụng biểu thức định luật ôm cho toàn mạch: \(I = \dfrac{E}{{{R_N} + r}}\)
+ Sử dụng biểu thức định luật ôm.
Câu hỏi khác
- Bài tập điện năng và công suất điện - định luật jun- lenxơ lý 11 có lời giải
- Bài tập định luật ôm đối với toàn mạch - mắc nguồn điện thành bộ lý 11 có lời giải
- Bài tập tính điện trở dây dẫn - biến trở có lời giải MÔN LÝ lớp 11
- Bài tập định luật ôm cho đoạn mạch chỉ có điện trở lý 11 có lời giải
- Bài tập đại cương về dòng điện không đổi - nguồn điện lý 11 có lời giải.
