Câu hỏi:
2 năm trước
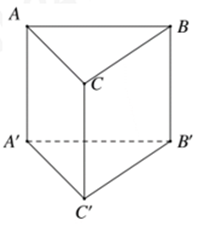
Cho khối lăng trụ đều \(ABC.A'B'C'\)có cạnh đáy bằng \(2a\), cạnh bên bằng \(3a\) (tham khảo hình vẽ bên). Tính thể tích của khối lăng trụ \(ABC.A'B'C'\).
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có: \({S_{ABC}} = \dfrac{{{{\left( {2a} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \).
Vậy \({V_{ABC.A'B'C'}} = {S_{ABC}}.AA' = {a^2}\sqrt 3 .3a = 3{a^3}\sqrt 3 \).
Hướng dẫn giải:
- Sử dụng công thức tính nhanh diện tích tam giác đều cạnh a là \(S = \dfrac{{{a^2}\sqrt 3 }}{4}\).
- Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là \(V = Bh\).


