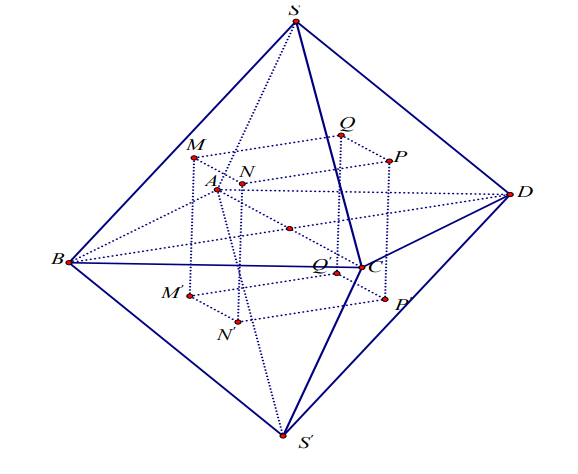
Cho khối bát diện đều có cạnh \(a\). Gọi \(M\), \(N\), \(P\), \(Q\) lần lượt là trọng tâm của các tam giác \(SAB,\) \(SBC\), \(SCD\), \(SDA\); gọi \(M'\), \(N'\), \(P'\), \(Q'\) lần lượt là trọng tâm của các tam giác \(S'AB\), \(S'BC\), \(S'CD\), \(S'DA\) (như hình vẽ dưới). Thể tích của khối lăng trụ \(MNPQ.M'N'P'Q'\) là
Trả lời bởi giáo viên
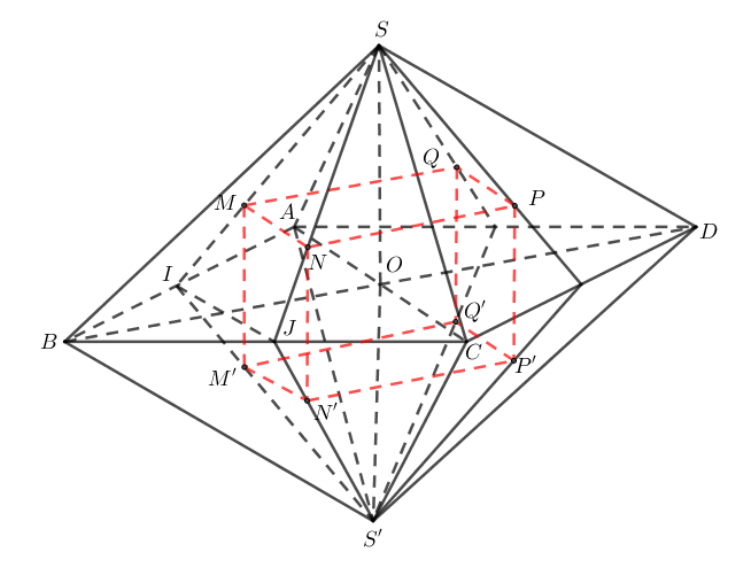
Gọi \(O = AC \cap BD\); \(I\), \(J\) lần lượt là trung điểm của \(AB\), \(BC\).
Do \(M\), \(N\) lần lượt là trọng tâm của các tam giác \(SAB\), \(SBC\) nên ta có \(MN = \dfrac{2}{3}IJ = \dfrac{1}{3}AC = \dfrac{{a\sqrt 2 }}{3}\).
Do \(SABCDS'\) là bát diện đều nên hoàn toàn tương tự ta có tất cả các cạnh còn lại của khối lăng trụ \(MNPQ.M'N'P'Q'\) cũng bằng \(\dfrac{{a\sqrt 2 }}{3}\).
Mặt khác \(AC \bot BD\) mà \(MN\,{\rm{//}}\,AC\,{\rm{//}}\,PQ\), \(MQ\,{\rm{//}}\,BD\,{\rm{//}}\,NP\) nên \(MNPQ\) là hình vuông.
Tương tự ta có tất cả các mặt còn lại của lăng trụ \(MNPQ.M'N'P'Q'\) cũng là hình vuông.
Suy ra lăng trụ \(MNPQ.M'N'P'Q'\) là hình lập phương có cạnh \(\dfrac{{a\sqrt 2 }}{3}\).
Vậy \({V_{MNPQ.M'N'P'Q'}} = {\left( {\dfrac{{a\sqrt 2 }}{3}} \right)^3} = \dfrac{{2{a^3}\sqrt 2 }}{{27}}\).
Hướng dẫn giải:
- Tính cạnh của hình lập phương
- Tính thể tích hình lập phương