Câu hỏi:
2 năm trước
Cho hình vuông ABCD có cạnh \(20cm\). Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng \(\dfrac{3}{4}\) diện tích hình vuông ABCD.
Trả lời bởi giáo viên
Đáp án đúng: d
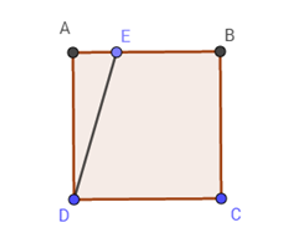
Gọi \(BE = x\,\,(m)\).
Diện tích hình vuông ABCD là:
\({S_{ABCD}} = A{B^2} = {20^2} = 400\left( {{m^2}} \right)\).
Diện tích hình thang vuông BCDE là:
\({S_{BCDE}} = \dfrac{{\left( {BE + DC} \right)BC}}{2} = \dfrac{{\left( {x + 20} \right).20}}{2} = 10\left( {x + 20} \right)\).
Vì diện tích hình thang vuông BCDE bằng \(\dfrac{3}{4}\) diện tích hình vuông ABCD nên ta có:
\({S_{BCDE}} = \dfrac{3}{4}.{S_{ABCD}} \Leftrightarrow 10(x + 20) = \dfrac{3}{4}.400 \Leftrightarrow x + 20 = 30 \Leftrightarrow x = 10\,(cm)\).
Vậy điểm E ở trên cạnh AB sao cho \(BE = 10\,cm\) hay \(E\) là trung điểm đoạn \(AB.\)
Hướng dẫn giải:
Gọi độ dài đoạn BE là x.
Lập công thức tính diện tích hình vuông ABCD, hình thang BCDE.
Lập phương trình biểu thị mối quan hệ giữa hai diện tích, từ đó tìm ra độ dài đoạn BE và vị trí điểm E trên AB.
